题目内容
11.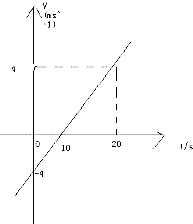 一质点沿某一直线运动,t=0时位于坐标原点,如图为质点做直线运动的速度一时间图象.求:
一质点沿某一直线运动,t=0时位于坐标原点,如图为质点做直线运动的速度一时间图象.求:(1)该质点的位移随时间变化的关系式;
(2)从t=0到t=20s内质点通过的位移和路程.
分析 (1)由图象的斜率求出加速度,再由位移时间公式求位移与时间的关系式.
(2)v-t图象与坐标轴围成面积代表位移,时间轴上方位移为正,时间轴下方位移为负.位移大小之和等于路程.
解答 解:(1)由运动图象可知:
初速度 v0=-5m/s,
加速度 a=$\frac{△v}{△t}$=$\frac{0-(-5)}{10}$=0.5m/s2.
所以质点的位移随时间变化的关系式为
x=v0t+$\frac{1}{2}a{t}^{2}$=(-5t+0.25t2)m
(2)由图象可知:t=0到t=20s内,t轴上方的面积等于t轴下方的面积,故位移为0,路程为 s=2×($\frac{1}{2}×10×5$)m=50m
答:
(1)该质点的位移随时间变化的关系式是 x=(-5t+0.25t2)m;
(2)从t=0到t=20s内质点通过的位移是0,路程是50m.
点评 本题是为速度-时间图象的应用,要明确斜率的含义,知道在速度-时间图象中图象与坐标轴围成的面积的含义.

练习册系列答案
相关题目
8.关于力和运动的关系,下列说法正确的是( )
| A. | 由m=$\frac{F}{a}$知,某一物体的质量跟其所受的合外力成正比 | |
| B. | 由a=$\frac{F}{m}$知,某一物体运动的加速度跟其质量成正比 | |
| C. | 物体运动方向一定跟其合外力方向相同 | |
| D. | 物体加速度方向一定跟其合外力方向相同 |
9.把一个导体放入匀强电场中,静电平衡时( )


| A. | 把一个负电荷从A移动到B,电场力做正功 | |
| B. | 三点的场强相比,EA=EB=EC | |
| C. | 三点的电势相比,φA>φB>φC | |
| D. | 导体内感应电荷的电场方向向左 |
16. 如图所示,线圈A接交流电源,其电流的表达式i=Imsin$\frac{2π}{T}$t,设交流电为正半周期时线圈A的上端电势高于下端电势,副线圈B接光滑导轨及光滑金属棒ab,导轨间的磁场方向如图.据此可知,在0-T时间内ab具有向右加速度的时间段是( )
如图所示,线圈A接交流电源,其电流的表达式i=Imsin$\frac{2π}{T}$t,设交流电为正半周期时线圈A的上端电势高于下端电势,副线圈B接光滑导轨及光滑金属棒ab,导轨间的磁场方向如图.据此可知,在0-T时间内ab具有向右加速度的时间段是( )
 如图所示,线圈A接交流电源,其电流的表达式i=Imsin$\frac{2π}{T}$t,设交流电为正半周期时线圈A的上端电势高于下端电势,副线圈B接光滑导轨及光滑金属棒ab,导轨间的磁场方向如图.据此可知,在0-T时间内ab具有向右加速度的时间段是( )
如图所示,线圈A接交流电源,其电流的表达式i=Imsin$\frac{2π}{T}$t,设交流电为正半周期时线圈A的上端电势高于下端电势,副线圈B接光滑导轨及光滑金属棒ab,导轨间的磁场方向如图.据此可知,在0-T时间内ab具有向右加速度的时间段是( )| A. | 0-$\frac{T}{4}$ | B. | $\frac{T}{4}$-$\frac{T}{2}$ | C. | $\frac{T}{2}$-$\frac{3T}{4}$ | D. | $\frac{3T}{4}$-T |
3. 用四个相同的小量程电流表,分别改装成了量程不同的大量程电流表A1、A2和量程不同的电压表V1、V2,若把电表分别采用并联的方式接入电路,如图(a)、(b)所示,则闭合开关后,下列有关说法正确的是( )
用四个相同的小量程电流表,分别改装成了量程不同的大量程电流表A1、A2和量程不同的电压表V1、V2,若把电表分别采用并联的方式接入电路,如图(a)、(b)所示,则闭合开关后,下列有关说法正确的是( )
 用四个相同的小量程电流表,分别改装成了量程不同的大量程电流表A1、A2和量程不同的电压表V1、V2,若把电表分别采用并联的方式接入电路,如图(a)、(b)所示,则闭合开关后,下列有关说法正确的是( )
用四个相同的小量程电流表,分别改装成了量程不同的大量程电流表A1、A2和量程不同的电压表V1、V2,若把电表分别采用并联的方式接入电路,如图(a)、(b)所示,则闭合开关后,下列有关说法正确的是( )| A. | 图(a)中的A1、A2的示数相同 | B. | 图(a)中的A1、A2的指针偏角相同 | ||
| C. | 图(b)中的V1、V2的示数相同 | D. | 图(b)中的V1、V2的指针偏角相同 |
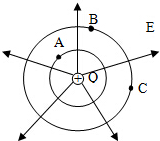 如图所示,是电荷量为Q的正点电荷形成的电场,箭头表示电场线方向,每一个圆面表示一个等势面,有一个电荷量为q的正点电荷从A点运动到B点再运动到C点,电场力做的总功为W,求:
如图所示,是电荷量为Q的正点电荷形成的电场,箭头表示电场线方向,每一个圆面表示一个等势面,有一个电荷量为q的正点电荷从A点运动到B点再运动到C点,电场力做的总功为W,求: