题目内容
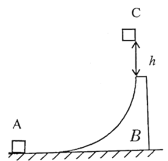
【题目】半径R=0.8m、质量为2m的
圆弧槽B静止于水平地面上，圆弧底端与地面相切，质量为7m的小滑块A静止于圆弧槽左侧。将质量为m的小滑块C从圆弧槽B顶端正上方h=0.4m处由静止释放。已知所有接触面均光滑，小滑块A、C均可视为质点，重力加速度g取10m/s2
（1）在小滑块C从释放到滑离圆弧槽B的过程中，求圆弧B的位移大小；
（2）小滑块C与小滑块A发生弹性碰撞（二者碰撞时间忽略不计）后，通过计算加以说明小滑块C能否追上B。
【答案】（1）
（2）能追上
【解析】
（1）BC组成的系统水平方向动量守恒，以向左为正方向，
由动量守恒定律得:
，①
则
②
又有
③
②③联立解得
（2）C、B组成的系统机械能守恒:
④
①④联立解得
⑤
C与A发生弹性碰撞，由C与A组成系统动量守恒得:
⑥
由机械能守恒得:
⑦
由⑤⑥⑦联立解得
由于
，所以C能追上B.
练习册系列答案
相关题目
