Question

【题目】如图所示，倾斜轨道AB的倾角为37°，CD、EF轨道水平，AB与CD通过光滑圆弧管道BC连接，CD右端与竖直光滑圆周轨道相连。小球可以从D进入该轨道，沿轨道内侧运动，从E滑出该轨道进入EF水平轨道。小球由静止从A点释放，已知AB长为5R，CD长为R，重力加速度为g，小球与斜轨AB及水平轨道CD、EF的动摩擦因数均为0．5，圆弧管道BC入口B与出口C的高度差为1．8R．。 （sin37°=0．6，cos37°=0．8）求：

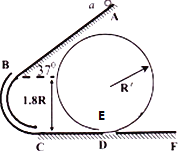
（1）小球滑到斜面底端C时速度的大小；

（2）小球对刚到C时对轨道的作用力；

（3）要使小球在运动过程中不脱离轨道，竖直圆周轨道的半径R′应该满足什么条件？若R′=2．5R，小球最后所停位置距D（或E）多远？（注：在运算中，根号中的数值无需算出）

Answer 1

【答案】（1）（2）6．6mg，方向竖直向下．（3）b球将停在D点左侧，距D点0．6R处．

【解析】

试题分析：（1）设小球到达C点时速度为v，a球从A运动至C过程，由动能定理有：

可得：

2）小球沿BC轨道做圆周运动，设在C点时轨道对球的作用力为N，由牛顿第二定律，有：

其中r满足： r+rsin53°=1．8R

联立上式可得： N=6．6mg

由牛顿第三定律可得，球对轨道的作用力为6．6mg，方向竖直向下．

（3球不脱离轨道，有两种情况：

情况一：小球能滑过圆周轨道最高点，进入EF轨道．则小球在最高点P应满足：

小球从C直到P点过程，由动能定理，有：

可得：

情况二：小球上滑至四分之一圆轨道的Q点时，速度减为零，然后滑回D．则由动能定理有：

解得：R′≥2．3R

若R′=2．5R，由上面分析可知，小球必定滑回D，设其能向左滑过DC轨道，并沿CB运动到达B点，在B点的速度为vB，则由能量守恒定律有：

可得：

故知，小球不能滑回倾斜轨道AB，小球将在两圆轨道之间做往返运动，小球将停在CD轨道上的某处．设小球在CD轨道上运动的总路程为S，则由能量守恒定律，有：

由上述两式，可得： S=5．6R

所以知，b球将停在D点左侧，距D点0．6R处．