题目内容
10.如图甲所示,MN、PQ为间距L=0.5m足够长的平行导轨,NQ⊥MN,导轨的电阻均不计.导轨平面与水平面间的夹角θ=37°,NQ间连接有一个R=4Ω的电阻.有一匀强磁场垂直于导轨平面且方向向上,磁感应强度为B0=1T.将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好.现由静止释放金属棒,当金属棒滑行至cd处时达到稳定速度,已知在此过程中通过金属棒截面的电量q=0.2C,且金属棒的加速度a与速度v的关系如图乙所示,设金属棒沿导轨向下运动过程中始终与NQ平行.(取g=10m/s2,sin37°=0.6,cos37°=0.8).求: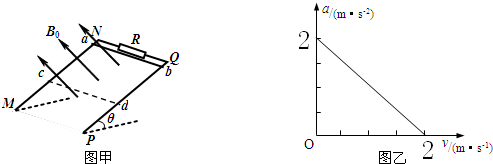
(1)金属棒与导轨间的动摩擦因数μ
(2)金属棒ab的电阻r以及cd离NQ的距离s
(3)金属棒滑行至cd处的过程中,电阻R上产生的热量
(4)若将金属棒滑行至cd处的时刻记作t=0,从此时刻起,让磁感应强度逐渐减小,为使金属棒中不产生感应电流,则磁感应强度B应怎样随时间t变化(写出B与t的关系式).
分析 (1)当刚释放时,导体棒中没有感应电流,所以只受重力、支持力与静摩擦力,由牛顿第二定律可求出动摩擦因数.
(2)当金属棒速度稳定时,则受到重力、支持力、安培力与滑动摩擦力达到平衡,这样可以列出安培力公式,产生感应电动势的公式,再由闭合电路殴姆定律,列出平衡方程可求出金属棒的内阻,从而利用通过棒的电量来确定发生的距离.
(3)金属棒滑行至cd处的过程中,由动能定理可求出安培力做的功,而由于安培力做功导致电能转化为热能.
(4)要使金属棒中不产生感应电流,则穿过线框的磁通量不变.同时棒受到重力、支持力与滑动摩擦力做匀加速直线运动.从而可求出磁感应强度B应怎样随时间t变化的.
解答 解:(1)当v=0时,a=2m/s2
由牛顿第二定律得:mgsinθ-μmgcosθ=ma
μ=0.5
(2)由图象可知:vm=2m/s
当金属棒达到稳定速度时,有FA=B0IL;
且B0IL+μmgcosθ=mgsinθ
解得I=0.2A;
切割产生的感应电动势:E=B0Lv=1×0.5×2=1V;
因I=$\frac{E}{R+r}$
解得r=1Ω
电量为:q=$\overline{I}$t=n $\frac{△∅}{R+r}$
而△∅=B0×L×s
联立解得:s=2m
(3)mgh-μmgscos37°-WF=$\frac{1}{2}$mv2-0
产生热量:WF=Q总=0.1J
${Q}_{R}=\frac{4}{5}$Q总=0.08J
(4)当回路中的总磁通量不变时,
金属棒中不产生感应电流.
此时金属棒将沿导轨做匀加速运动.
牛顿第二定律:mgsinθ-μmgcosθ=ma
a=g(sinθ-μcosθ)=10×(0.6-0.5×0.8)m/s2=2m/s2
磁通量为:∅=BL(s+vt+$\frac{1}{2}$at2)=B0Ls
则磁感应强度与时间变化关系:B=$\frac{{B}_{0}s}{s+vt+\frac{{at}^{2}}{2}}$=$\frac{2}{2+2t{+t}^{2}}$
答:(1)金属棒与导轨间的动摩擦因数为0.5;
(2)cd离NQ的距离2m;
(3)金属棒滑行至cd处的过程中,电阻R上产生的热量0.08J;
(4)若将金属棒滑行至cd处的时刻记作t=0,从此时刻起,让磁感应强度逐渐减小,为使金属棒中不产生感应电流,则磁感应强度随时间t变化为B=$\frac{2}{2+2t{+t}^{2}}$
点评 本题考查了牛顿运动定律、闭合电路殴姆定律,安培力公式、感应电动势公式,还有动能定理.同时当金属棒速度达到稳定时,则一定是处于平衡状态,原因是安培力受到速度约束的.还巧妙用磁通量的变化去求出面积从而算出棒的距离.最后线框的总磁通量不变时,金属棒中不产生感应电流是解题的突破点

| A. | 速度一定在不断地改变,加速度也一定在不断地改变,且加速度的改变乃速度变化的原因 | |
| B. | 速度一定在不断地改变,加速度可以不变,加速度乃速度不断改变的原因 | |
| C. | 速度大小可以不变,加速度一定在不断改变,且加速度的改变乃速度方向改变的原因 | |
| D. | 速度和加速度都可以不变,且速度方向为曲线上该点的切线方向 |
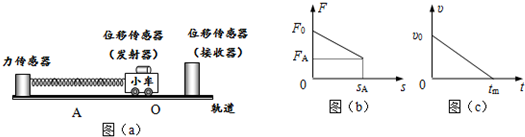
 在如图所示装置中,m1由轻质滑轮悬挂在绳间,两物体质量分别为m1、m2,悬点a、b间的距离远大于滑轮的直径,不计一切摩擦,整个装置处于静止状态,则( )
在如图所示装置中,m1由轻质滑轮悬挂在绳间,两物体质量分别为m1、m2,悬点a、b间的距离远大于滑轮的直径,不计一切摩擦,整个装置处于静止状态,则( )| A. | α一定等于β | B. | m1一定大于m2 | C. | m1可能等于2m2 | D. | m1不可能等于m2 |
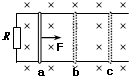 如图所示,水平面内两光滑的平行金属导轨的左端与电阻R相连接,在导轨所在的空间内有竖直向下匀强磁场,质量一定的金属棒垂直于导轨并与导轨接触良好.今对棒施加一个水平向右的外力F,使金属棒从a位置开始,向右做初速度为零的匀加速运动并依次通过位置b和c.若导轨与棒的电阻不计,ab=bc,则关于金属棒在运动过程中( )
如图所示,水平面内两光滑的平行金属导轨的左端与电阻R相连接,在导轨所在的空间内有竖直向下匀强磁场,质量一定的金属棒垂直于导轨并与导轨接触良好.今对棒施加一个水平向右的外力F,使金属棒从a位置开始,向右做初速度为零的匀加速运动并依次通过位置b和c.若导轨与棒的电阻不计,ab=bc,则关于金属棒在运动过程中( )| A. | 棒通过b、c两位置时,电阻R的电功率之比为1:2 | |
| B. | 棒通过b、c两位置时,电阻R的电流之比为1:2 | |
| C. | 在从a到b与从b到c的两个过程中,电阻R上产生的热量相同 | |
| D. | 在从a到b与从b到c的两个过程中,通过棒的横截面的电量相同 |
 如图甲所示,绝缘轻质细绳一端固定在方向相互垂直的匀强电场和匀强磁场中的O点,另一端连接带正电的小球,小球电荷量q=6×10-7C,在图示坐标中,电场方向沿竖直方向,坐标原点O的电势为零.当小球以2m/s的速率绕O点在竖直平面内做匀速圆周运动时,细绳上的拉力刚好为零.在小球从最低点运动到最高点的过程中,轨迹上每点的电势φ随纵坐标y的变化关系如图乙所示,重力加速度g=10m/s2.则下列判断正确的是( )
如图甲所示,绝缘轻质细绳一端固定在方向相互垂直的匀强电场和匀强磁场中的O点,另一端连接带正电的小球,小球电荷量q=6×10-7C,在图示坐标中,电场方向沿竖直方向,坐标原点O的电势为零.当小球以2m/s的速率绕O点在竖直平面内做匀速圆周运动时,细绳上的拉力刚好为零.在小球从最低点运动到最高点的过程中,轨迹上每点的电势φ随纵坐标y的变化关系如图乙所示,重力加速度g=10m/s2.则下列判断正确的是( )| A. | 匀强电场的场强大小为3.2×106v/m | |
| B. | 小球重力势能增加最多的过程中,电势能减少了0.024J | |
| C. | 小球做顺时针方向的匀速圆周运动 | |
| D. | 小球所受的洛伦兹力的大小为0.03N |
 家用电热灭蚊器电热部分的主要器件是PCT元件,PCT元件是由钛酸钡等导体材料制成的电阻器,其电阻率ρ与温度t的关系如图所示.由于这种特性,PCT元件具有发热、控温双重功能.对此,以下判断中正确的是( )
家用电热灭蚊器电热部分的主要器件是PCT元件,PCT元件是由钛酸钡等导体材料制成的电阻器,其电阻率ρ与温度t的关系如图所示.由于这种特性,PCT元件具有发热、控温双重功能.对此,以下判断中正确的是( )| A. | 通电后,其电功率先增大后减小 | |
| B. | 通电后,其电功率先减小后增大 | |
| C. | 当其产生的热量与散发的热量相等时,温度保持在t1或t2不变 | |
| D. | 当其产生的热量与散发的热量相等时,温度保持在t1至t2间的某一值不变 |
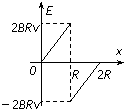
 如图所示,xOy平面内有一半径为R的圆形区域,区域内有磁感应强度大小为B的匀强磁场,左半圆磁场方向垂直于xOy平面向里,右半圆磁场方向垂直于xOy平面向外.一平行于y轴的长导体棒ab以速度v沿x轴正方向做匀速运动,则导体棒ab两端的感应电动势E(取b点电势高时为正)与导体棒位置x关系的图象是( )
如图所示,xOy平面内有一半径为R的圆形区域,区域内有磁感应强度大小为B的匀强磁场,左半圆磁场方向垂直于xOy平面向里,右半圆磁场方向垂直于xOy平面向外.一平行于y轴的长导体棒ab以速度v沿x轴正方向做匀速运动,则导体棒ab两端的感应电动势E(取b点电势高时为正)与导体棒位置x关系的图象是( )