题目内容
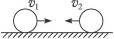
如图,一质量m = 1 kg的木块静止的光滑水平地面上。开始时,木块右端与墙相距L = 0.08 m;质量为m = 1 kg的小物块以初速度υ0= 2 m/s滑上木板左端。木板长度可保证物块在运动过程中不与墙接触。物块与木板之间的动摩擦因数为μ= 0.1,木板与墙的碰撞是完全弹性的。取g = 10 m/s2,求

小题1:从物块滑上木板到两者达到共同速度时,木板与墙碰撞的次数及所用的时间;
小题2:达到共同速度时木板右端与墙之间的距离。

小题1:从物块滑上木板到两者达到共同速度时,木板与墙碰撞的次数及所用的时间;
小题2:达到共同速度时木板右端与墙之间的距离。
小题1:1.8S
小题2:0.06 m
(1)物块滑上木板后,在摩擦力作用下,木板从静止开始做匀加速运动。设木块加速度为a,经历时间T后与墙第一次碰撞,碰撞时的速度为υ1,则
μmg=ma ①
L=aT2 ②
υ1=at ③
联立①②③式解得T= 0.4 s υ1 = 0.4 m/s ④
在物块与木板两者达到共同速度前,在每两次碰撞之间,木板受到物块对它的摩擦力作用而做加速度恒定的运动,因而木板与墙相碰后将返回至初态,所用时间为T。设在物块与木板两者达到共同速度υ前木块共经历n次碰撞,则有
υ= υ0– (2nT + △t)a=a△t ⑤
式中△t是碰撞n次后木板从起始位置至达到共同速度所需要的时间。
⑤式可改写为2υ= υ0– 2nT ⑥
由于木板的速率只能位于0到v0之间,故有0 ≤ υ0– 2nT ≤ 2υ0 ⑦
求解上式得
1.5 ≤ n ≤ 2.5
由于n是整数,故 n=2 ⑧
再由①⑤⑧得
△t= 0.2 s ⑨
υ = 0.2m/s ⑩
从开始到物块与木板两者达到共同速度所用的时间为t= 4T + △t= 1.8 s
(2)物块与木板达到共同速度时,木板右端与墙之间的距离为 s=L–a△t2
联立①12式,并代入数据得s= 0.06m
μmg=ma ①
L=aT2 ②
υ1=at ③
联立①②③式解得T= 0.4 s υ1 = 0.4 m/s ④
在物块与木板两者达到共同速度前,在每两次碰撞之间,木板受到物块对它的摩擦力作用而做加速度恒定的运动,因而木板与墙相碰后将返回至初态,所用时间为T。设在物块与木板两者达到共同速度υ前木块共经历n次碰撞,则有
υ= υ0– (2nT + △t)a=a△t ⑤
式中△t是碰撞n次后木板从起始位置至达到共同速度所需要的时间。
⑤式可改写为2υ= υ0– 2nT ⑥
由于木板的速率只能位于0到v0之间,故有0 ≤ υ0– 2nT ≤ 2υ0 ⑦
求解上式得
1.5 ≤ n ≤ 2.5
由于n是整数,故 n=2 ⑧
再由①⑤⑧得
△t= 0.2 s ⑨
υ = 0.2m/s ⑩
从开始到物块与木板两者达到共同速度所用的时间为t= 4T + △t= 1.8 s
(2)物块与木板达到共同速度时,木板右端与墙之间的距离为 s=L–a△t2
联立①12式,并代入数据得s= 0.06m

练习册系列答案
相关题目
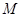 =0.4kg的砂箱A、B并排放在光滑的水平桌面上,一颗质量为
=0.4kg的砂箱A、B并排放在光滑的水平桌面上,一颗质量为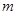 =0.1kg的子弹以
=0.1kg的子弹以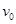 =140m/s的水平速度射向
=140m/s的水平速度射向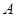 ,如图所示.射穿
,如图所示.射穿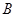 并同
并同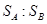 =1∶2,求:
=1∶2,求: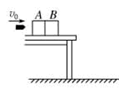
 .
.