题目内容
14.某时刻绿车和红车位于同一出发点,绿车以15m/s的速度匀速行驶,2s后红车才从静止开始以3m/s2的加速度开始启动追赶绿车,问:(1)两车何时相遇?
(2)何时两车相距最远,最大距离是多少?
分析 (1)相遇时两车相对出发点位移相等,据位移关系求得何时相遇;
(2)两车相距最远时,两车速度相等,据此求得时间和最大距离.
解答 解:(1)两车相遇时相对出发点的位移相等,根据位移时间关系有:
$15t=\frac{1}{2}a(t-2)^{2}$
解得:t=$7±3\sqrt{5}$s,时间负值不合题意,故t=$7+3\sqrt{5}s$
(2)当两车速度相等时两车相距最远,此时绿车运动时间t${t}_{1}=2+\frac{15}{3}s=7s$
此时绿车的位移x1=15×7m=105m
红车位移:${x}_{2}=\frac{1}{2}×3×(7-2)^{2}m=37.5m$
两车相距最大距离为:△x=x1-x2=105-37.5m=67.5m
答:(1)绿车出发后$7+3\sqrt{5}s$时两车相遇;
(2)绿车出发后7s两车相距最远,最大距离是67.5m.
点评 追击相遇问题主要从位移角度入手解题,知道两车相距最远或最近的临界条件是两车速度相等是解决问题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
2.(多选)关于匀速圆周运动的说法,正确的是( )
| A. | 匀速圆周运动的速度大小保持不变,所以做匀速圆周运动的物体没有加速度 | |
| B. | 做匀速圆周运动的物体,虽然速度大小不变,但方向时刻都在改变,所以必有加速度 | |
| C. | 做匀速圆周运动的物体,加速度的大小保持不变,所以是匀变速曲线运动 | |
| D. | 匀速圆周运动加速度的方向时刻都在改变,所以匀速圆周运动一定是变加速曲线运动 |
 某同学要测量一均匀新材料制成的圆柱体的电阻率ρ.步骤如下:
某同学要测量一均匀新材料制成的圆柱体的电阻率ρ.步骤如下:
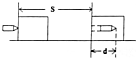 飞行子弹打入放在光滑水平面上的木块中深入2cm,未穿出同时木块滑动了1cm,则子弹动能的变化、木块获得的动能、由于摩擦增加的内能的比是多少?
飞行子弹打入放在光滑水平面上的木块中深入2cm,未穿出同时木块滑动了1cm,则子弹动能的变化、木块获得的动能、由于摩擦增加的内能的比是多少?
