题目内容
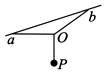
【题目】如图所示，从倾角为θ的斜面上某点先后将同一小球以不同的初速度水平抛出，小球均落在斜面上，当抛出的初速度为v01时，小球经时间t1离斜面最远，最后到达斜面时速度方向与斜面的夹角为α1；当抛出的初速度为v02时，小球经时间t2离斜面最远，最后到达斜面时速度方向与斜面的夹角为α2，则（ ）
A. 若v01＞v02时，α1＞α2，t1＞t2．
B. 若v01＞v02时，α1＜α2，t1＜t2．
C. 若v01＜v02时，t1＜t2．α1=α2
D. α1、α2的关系与斜面的倾角θ有关
【答案】CD
【解析】设当将小球以初速度v0平抛时，在斜面上的落点与抛出点的间距为L，则由平抛运动的规律得Lcosθ=v0t，Lsinθ＝
gt2，tanθ＝
，速度与水平方向的夹角为β，则tanβ＝
＝2tanθ，因为θ一定，则β一定，所以小球到达斜面时速度方向与斜面的倾角α=β-θ一定．所以α1=α2．当速度方向与斜面平行时，距离斜面最远，此时vy=v0tanθ=gt，则t=
，知初速度越大，距离斜面最远的时间越长．故CD正确，AB错误．故选CD．
练习册系列答案
相关题目
