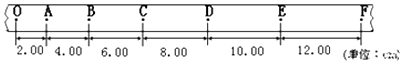��Ŀ����
����Ŀ����ͼ��ʾ��ϸ���ȵ�U�β�������ֱ���ã������ˮ������ų�L=13cm���������壬�Ҷ˿��ڣ������������¶�T=312Kʱ������ˮ����ĸ߶Ȳ��h=4cm���ֶԷ�����建�����ȣ�ֱ�����������е�ˮ������ƽ����������ѹpo=76cmHg��
�������������е�ˮ������ƽʱ���������¶ȣ�
�������֢����������¶Ȳ��䣬���ҹܵĿ��ڶ˻���ע��ˮ����ֱ���Ҳ�ܵ�ˮ��������ܵĸߡ�h��=4cm����ע��ˮ�����ij��ȣ�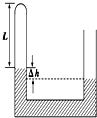
���𰸡��⣺���貣���ܷ�������̬ѹǿΪp�����ΪV�������ܵĺ�����ΪS��ĩ̬ѹǿΪp�䣬���ΪV�䣬���¶�������T��ʱ�����������е�ˮ������ƽ��������������״̬���̿ɵã�![]()
������ɵã�p=��76��4��cmHg=72cmHg
V=LS ![]() V��=L��S
V��=L��S ![]()
���T��=380K
����ע���ˮ������Ϊxʱ���Ҳ�ܵ�ˮ��������ܵĸߡ�h�䣮ĩ״̬������������ѹǿ![]() �����V��=L��S
�����V��=L��S
���ݲ�������ɿɵã�p��V��=p��V��
��ã�L��=14.25cm
x=��h��+2��L�䩁L�壩
��ã�x=5.5cm
�𣺢������������е�ˮ������ƽʱ���������¶�Ϊ380K��
�������֢����������¶Ȳ��䣬���ҹܵĿ��ڶ˻���ע��ˮ����ֱ���Ҳ�ܵ�ˮ��������ܵĸߡ�h��=4cm����ע��ˮ�����ij���5.5cm��
���������ٷֱ������������̬��ĩ̬��ѹǿ������̬��������������¶ȣ��ڱ��֢����������¶Ȳ��䣬Ϊ��ʹ���������е�ˮ����߶Ȳ�Ϊ��h=4cm������ҹܵĿ��ڶ��ٻ���ע��ˮ����������巢�����±仯��ˮ������ƽʱ����������ѹǿ���ڴ���ѹ���ɲ�������ɺͼ��ι�ϵ���ע��ˮ��������

 ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д� С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д�����Ŀ��ijͬѧ̽�������뵯���쳤���Ĺ�ϵ��
�ٵ�����Ȼ���ң������ɾ�ֹʱ�����ȼ�ΪL0�������¶˹���������ʱ�����ȼ�ΪLx������������ÿ������10g���룬���ɳ������μ�ΪL1��L6 �� ���������
�������� | L0 | Lx | L1 | L2 | L3 | L4 | L5 | L6 |
��ֵ | 25.35 | 27.35 | 29.34 | 31.31 | 33.40 | 35.35 | 37.40 | 39.30 |
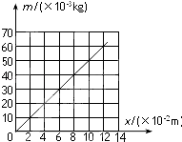
����ͼ�Ǹ�ͬѧ���ݱ�����������ͼ������������������������ǵ��ɳ������IJ�ֵ���L0����Lx������
����ͼ��֪���ɵľ���ϵ��Ϊ N/m��ͨ��ͼ�ͱ���֪�����̵�����Ϊ g�����������λ��Ч���֣��������ٶ�ȡ10m/s2����