��Ŀ����
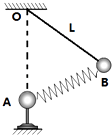
����Ŀ����ͼ��ʾ������ˮƽ�������ǿ�糡����һ�̶���O����һ������Ϊl=0.20m�ľ�Ե���߰�����Ϊm=0.10kg����������ɵĽ���С��������O�㣬С��ֹ��B��ʱ��������ֱ����ļн�Ϊ��=37�㣮�ֽ�С������λ��A��ʹ����ˮƽ�Ž����ɾ�ֹ�ͷţ�gȡ10m/s2 �� sin37��=0.60��cos37��=0.80����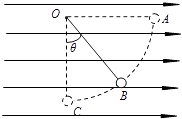
��1��С�����ܵ糡���Ĵ�С��
��2��С��ͨ����͵�Cʱ���ٶȴ�С��
��3��С��ͨ����͵�Cʱ���߶�С���������С��
���𰸡�
��1��
�⣺С��������mg���糡��F������T���侲ֹʱ�������ͼ2��ʾ��
���ݹ�����ƽ�������У�F=mgtan37��=0.75N

��2��
�⣺��С����͵�ʱ���ٶ�Ϊv��С���ˮƽλ���˶�����͵�Ĺ����У����ݶ��ܶ����У�mgl��Fl= ![]() mv2
mv2
��ã�v= ![]() =1.0m/s
=1.0m/s
��3��
�⣺��С��ͨ����͵�Cʱϸ�߶�С���������СΪT�䣮
����ţ�ٵڶ������У�T�䩁mg= ![]()
��ã�T��=1.5N
����������1��С����B�㴦�ھ�ֹ״̬����С�������������������ƽ������������⣻��2����С���A���˶���C��Ĺ��������ö��ܶ������ɽ��⣻��3����C�㣬С����������ϸ�ߵĺ����ṩ��������������������ʽ������⣮
�����㾫�������ն��ܶ������ۺ�Ӧ���ǽ����ĸ�������Ҫ֪��Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݣ�