Question

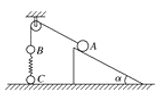
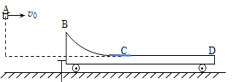
【题目】如图所示，一质量M=4kg的小车静置于光滑水平地面上，左侧用固定在地面上的销钉挡住。小车上表面由光滑圆弧轨道BC和水平粗糙轨道CD组成，BC与CD相切于C，圆弧BC所对圆心角θ＝37°，圆弧半径R=2.25m，滑动摩擦因数μ=0.48。质量m=1kg的小物块从某一高度处的A点以v0＝4m/s的速度水平抛出，恰好沿切线方向自B点进入圆弧轨道，最终与小车保持相对静止。取g＝10m/s2，sin37°=0.6，忽略空气阻力，求:

（1）A、B间的水平距离；

（2）物块通过C点时，轨道对物体的支持力；

（3）物块与小车因摩擦产生的热量。

Answer 1

【答案】（1）1.2m（2）（3）13.6J

【解析】

（1）物块从A到B由平抛运动的规律得:

tanθ=

x= v0t

得x=1.2m

（2）物块在B点时，由平抛运动的规律得：

物块在小车上BC段滑动过程中，由动能定理得： mgR(1－cosθ)＝mvC2－mvB2

在C点对滑块由牛顿第二定律得

联立以上各式解得：

（3）根据牛顿第二定律，对滑块有μmg＝ma1，

对小车有μmg＝Ma2

当滑块相对小车静止时，两者速度相等，即 vC－a1t1＝a2t1

由以上各式解得 ，

此时小车的速度为v＝a2t1＝

物块在CD段滑动过程中由能量守恒定律得：mvC2＝（M＋m）v2 + Q

解得：Q=13.6J