题目内容

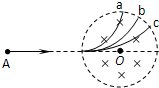
如图，在一矩形区域内不加磁场时，不计重力的带电粒子以某一初速度垂直左边界射入，穿过此区域的时间为t．若加上磁感应强度为B?水平向外的匀强磁场，带电粒子仍以原来的初速度入射，粒子飞出时偏离原方向60°．利用以上数据求出下列物理A．带电粒子的比荷B．带电粒子在磁场中运动的周期．
由带电粒子在磁场中运动的偏向角，可知带电粒子运动轨迹所对的圆心角为60°，因此由几何关系有：l=Rsin 60°；
由Bqv0=m
v02
R

得：R=
mv0
qB

故：l=
mv0
qB
sin 60°，
又未加磁场时有l=v0t，所以可求得：
比荷为：
q
m
=
sin60°
Bt
=
3
2Bt
．
周期为：T=
2πR
v0
=
2πm
qB
=
4
3
πt
3
；
答：带电粒子的比荷为
3
2Bt
；带电粒子在磁场中运动的周期为
4
3
πt
3
．
练习册系列答案
相关题目
如图所示，一束质量为m、电荷量为q的带正电粒子从O点由静止开始经过匀强电场加速后，均从边界AN的中点P垂直于AN和磁场方向射入磁感应强度为B=
3
R
2mU
q
的匀强磁场中．已知匀强电场的宽度为d=
1
2
R，匀强磁场由一个长为2R、宽为
1
2
R的矩形区域组成，磁场方向垂直纸面向里，粒子间的相互作用和重力均不计．
（1）若加速电场加速电压为9U，求粒子在电磁场中运动的总时间；
（2）若加速电场加速电压为U，求粒子在电磁场中运动的总时间．
如图所示，带电平行金属板PQ和MN之间的距离为d；两金属板之间有垂直纸面向里的匀强磁场，磁感应强度大小为B．建立如图所示的坐标系，x轴平行于金属板，且与金属板中心线重合，y轴垂直于金属板．区域I的左边界是y轴，右边界与区域II的左边界重合，且与y轴平行；区域II的左、右边界平行．在区域I和区域II内分别存在匀强磁场，磁感应强度大小均为B，区域I内的磁场垂直于Oxy平面向外，区域II内的磁场垂直于Oxy平面向里．一电子沿着x轴正向以速度v0射入平行板之间，在平行板间恰好沿着x轴正向做直线运动，并先后通过区域I和II．已知电子电量为e，质量为m，区域I和区域II沿x轴方向宽度均为
3
mv0
2Be
．不计电子重力．
（1）求两金属板之间电势差U；
（2）求电子从区域II右边界射出时，射出点的纵坐标y；
（3）撤除区域I中的磁场而在其中加上沿x轴正向的匀强电场，使得该电子刚好不能从区域II的右边界飞出．求电子两次经过y轴的时间间隔t．
如图所示，圆形区域内有垂直纸面向内的匀强磁场，三个质量和电荷量都相同的带电粒子a、b、c，以不同的速率对准圆心O沿着AO方向射入磁场，其运动轨迹如图．若带电粒子只受磁场力的作用，则下列说法错误的是（　　）
A．三个粒子都带正电荷
B．c粒子速率最小
C．c粒子在磁场中运动时间最短
D．它们做圆周运动的周期Ta=Tb=Tc
如图，在空间中有一坐标系xOy，其第一象限内充满着两个匀强磁场区域I和II，直线OP是它们的边界，区域I中的磁感应强度为B，方向垂直纸面向外；区域II中的磁感应强度为2B，方向垂直纸面向内，边界上的P点坐标为（4L，3L）．一质量为m电荷量为q的带正粒子从P点平行于y轴负方向射入区域I，经过一段时间后，粒子恰好经过原点O，忽略粒子重力，已知sin37°=0.6，cos37°=0.8．求：
（1）粒子从P点运动到O点的时间为多少？
（2）粒子的速度大小是多少？
如图a所示，水平直线MN下方有竖直向上的匀强电场，现将一重力不计、比荷
q
m
=106C/kg的正电荷置于电场中的O点由静止释放，经过
π
15
×10-5s后，电荷以v0=1.5×l04m/s的速度通过MN进入其上方的匀强磁场，磁场与纸面垂直，磁感应强度B按图b所示规律周期性变化（图b中磁场以垂直纸面向外为正，以电荷第一次通过MN时为t=0时刻）．求：
（1）匀强电场的电场强度E
（2）图b中t=
4π
5
×10-5s时刻电荷与O点的水平距离
（3）如果在O点右方d=68cm处有一垂直于MN的足够大的挡板，求电荷从O点出发运动到挡板所需的时间．（sin37°=0.60，cos37°=0.80）
如图所示，水平绝缘地面上有一底部带有小孔的绝缘弹性竖直挡板AC，板高h=9cm，与A端等高处有一水平放置的篮筐，圆形筐口的圆心M离挡板的距离L=3m，AC左端及A端与筐口的连线上方存在匀强磁场和匀强电场，磁场方向垂直纸面向里，磁感应强度B=1T；现有一质量m=1×10-3kg、电量q=-1×10-3C、直径略小于小孔宽度的带电小球（视为质点），以某一速度从C端水平射入场中做匀速圆周运动．若球可直接从M点落入筐中，也可与AC相碰后从M点落入筐中，且假设球与AC相碰后以原速率沿碰前速度的反方向弹回弹回，碰撞时间不计，碰撞时电荷量不变，忽略小球运动对电场、磁场的影响．（g=10m/s2，sin53°=0.8），求：
（1）电场强度的大小与方向；
（2）小球运动的最大速率；
（3）若小球与AC碰撞1次后从M点落入筐中，求小球在电场和磁场共存的区域运动的时间（结果中可保留π）．
如图所示，边长为L的正方形PQMN区域内（含边界）有垂直于纸面向外的匀强磁场，左侧有水平向右的匀强电场，场强大小为E．质量为m、电荷量为q的带正电粒子从O点由静止开始释放，OPQ三点在同一水平直线上，OP=L，带电粒子从边界NM上的O′点离开磁场，O′与N点距离为
L
3
，则磁场磁感应强度的可能数值为（不计带电粒子重力）（　　）
A．
9
5
2mE
qL
B．3
2mE
qL
C．
12
5
2mE
qL
D．2
2mE
qL
如图所示，条形区域AA′BB′中存在方向垂直于纸面向外的匀强磁场，磁感应强度B的大小为0.3T，AA′、BB′为磁场边界，它们相互平行，条形区域的长度足够长，宽度d=1m．一束带正电的某种粒子从AA′上的O点以沿着与AA′成60°角、大小不同的速度射入磁场，当粒子的速度小于某一值v0时，粒子在磁场区域内的运动时间t0=4×10-6s；当粒子速度为v1时，刚好垂直边界BB′射出磁场．取π=3，不计粒子所受重力．求：
（1）粒子的比荷
q
m
；
（2）速度v0和v1的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网