题目内容
14.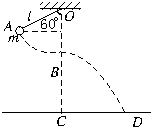 如图所示,让摆球从图中的A位置由静止开始下摆,正好摆到最低点B位置时线恰好被拉断.设摆线长L=1.6m,摆球质量为0.5kg,悬点与地面的竖直高度为H=4.0m,不计空气阻力,g=10m/s2.求:
如图所示,让摆球从图中的A位置由静止开始下摆,正好摆到最低点B位置时线恰好被拉断.设摆线长L=1.6m,摆球质量为0.5kg,悬点与地面的竖直高度为H=4.0m,不计空气阻力,g=10m/s2.求:(1)摆线承受的最大拉力
(2)摆球落地时速度的大小;
(3)D点到C点的距离.
分析 (1)小球从A点到B点的过程中,由机械能守恒定律求解小球经过B点时的速度大小,摆球摆到最低点B位置时,由牛顿第二定律求解细线能承受的最大拉力.
(2)细线被拉断后,摆球做平抛运动,平抛运动的高度为h=H-L=2.4m,再根据运动的分解法,由运动学公式求出小球落地时的速度大小.
(3)运用运动的分解方法求出平抛运动的水平距离DC.
解答 解:(1)小球从A点到B点的过程中,由机械能守恒定律有:
mgL(1-cosθ)=$\frac{1}{2}m{v}_{B}^{2}$
代入数据可解得:vB=$\sqrt{2gL(1-cosθ)}$=$\sqrt{2×10×1.6×(1-cos60°)}$=4m/s
摆球摆到最低点B位置时,由牛顿第二定律可知:
Fm-mg=m$\frac{{v}_{B}^{2}}{L}$
解得:Fm=m(g+$\frac{{v}_{B}^{2}}{L}$)=0.5×(10+$\frac{{4}^{2}}{1.6}$)N=10N
(2)小球离开B点后,作平抛运动,
竖直方向;H-L=$\frac{1}{2}g{t}^{2}$,得 t=$\sqrt{\frac{2(H-h)}{g}}$=$\sqrt{\frac{2×(4-1.6)}{10}}$s=0.4$\sqrt{3}$s
落地时竖直方向的速度:vy=gt=4$\sqrt{3}$m/s
落地时的速度大小:v=$\sqrt{{v}_{B}^{2}+{v}_{y}^{2}}$=$\sqrt{{4}^{2}+(4\sqrt{3})^{2}}$m/s=8m/s
(3)落地点D到C的距离
S=vBt
可解得:s=4×0.4$\sqrt{3}$m=$\frac{8}{5}\sqrt{3}$m
答:(1)细线能承受的最大拉力是10N;
(2)摆球落地时速度的大小是8m/s;
(3)D点到C点的距离是$\frac{8}{5}\sqrt{3}$m.
点评 本题是圆周运动与平抛运动的综合,采用程序法分析求解.对于第3问题,也可以根据机械能守恒定律求解.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案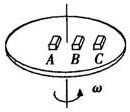 如图所示,A、B、C三个物体放在旋转圆台上,动摩擦因数均为μ,A的质量是2m,B和C的质量均为m,A、B离轴的距离为R,C离轴的距离为2R,当圆台旋转时,则( )
如图所示,A、B、C三个物体放在旋转圆台上,动摩擦因数均为μ,A的质量是2m,B和C的质量均为m,A、B离轴的距离为R,C离轴的距离为2R,当圆台旋转时,则( )| A. | 若A、B、C均未滑动,则C的向心加速度最大 | |
| B. | 若A、B、C均未滑动,则B所受的摩擦力最小 | |
| C. | 当圆台转速增大时,B比A先滑动 | |
| D. | 当圆台转速增大时,A比C先滑动 |
 在探究“质量一定,加速度a与合外力F的关系”实验中.
在探究“质量一定,加速度a与合外力F的关系”实验中.某学生根据实验数据作出了如图所示的a-F图象,其中图线不过原点并在末端发生了弯曲,产生这种现象的原因可能有( )
| A. | 在平衡摩擦力时,木板一端垫起的高度偏大 | |
| B. | 在平衡摩擦力时,木板一端垫起的高度偏小 | |
| C. | 盘和重物 的总质量m远小于车和砝码的总质量M | |
| D. | 盘和重物的总质量m不远小于车和砝码的总质量M |
| A. | 汽车在长直斜坡上匀速下滑时,机械能守恒 | |
| B. | 做平抛运动的小球,机械能守恒 | |
| C. | 外力对物体做功为零,物体的机械能一定守恒 | |
| D. | 物体所受合力不等于零,它的机械能一定不守恒 |
| A. | 3N,4N,5N | B. | 6N,10N,1N | C. | 9N,9N,9N | D. | 3N,5N,8N |
 如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,在杆上P点固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套有一质量m=2kg小球A,半径R=0.3m的光滑半圆形细轨道,竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量也为m=2kg的小球B,用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来,杆和半圆形轨道在同一竖直面内,两小球均可看做质点,且不计滑轮大小的影响,(g=10m/s2),现给小球A一个水平向右的恒力F=55N.求:
如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,在杆上P点固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套有一质量m=2kg小球A,半径R=0.3m的光滑半圆形细轨道,竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量也为m=2kg的小球B,用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来,杆和半圆形轨道在同一竖直面内,两小球均可看做质点,且不计滑轮大小的影响,(g=10m/s2),现给小球A一个水平向右的恒力F=55N.求:
 在探究“加速度与力、质量的关系”实验中,小明分别用物体A、B做了加速度随着外力的变化关系实验,如图(1)所示,用不同的重物P分别挂在光滑的动滑轮拉物体A、B,处理数据后,他们得到加速度a与弹簧秤弹力F的关系图象如图(2)所示,由图象可知
在探究“加速度与力、质量的关系”实验中,小明分别用物体A、B做了加速度随着外力的变化关系实验,如图(1)所示,用不同的重物P分别挂在光滑的动滑轮拉物体A、B,处理数据后,他们得到加速度a与弹簧秤弹力F的关系图象如图(2)所示,由图象可知