题目内容
4.长度为L1的列车甲以速度v1在平直铁轨上匀速行驶,长度为L2的列车乙以速度v2行驶的铁轨平行的另一铁轨上匀速相向行驶.则从两车车头对齐至车尾对齐这段时间里,求:(1)两车运动的位移大小之和?
(2)这段时间是多少?(答案用题中字母表示)
分析 根据几何关系求出两车运动的位移之和,即可得出甲车相对乙车运动的路程,结合甲车相对乙车的速度大小,求出从两车车头对齐至车尾对齐的时间.
解答 解:(1)两车运动的位移大小之和为:x=L1+L2.
(2)当两列火车反向行驶时,甲相对于乙的速度为:v=v1+v2,
甲与乙从相遇到离开要走的路程:s=L1+L2,
从两车车头对齐至车尾对齐经历的时间为:t=$\frac{{L}_{1}+{L}_{2}}{{v}_{1}+{v}_{2}}$.
答:(1)两车运动的位移大小之和为L1+L2.
(2)这段时间为$\frac{{L}_{1}+{L}_{2}}{{v}_{1}+{v}_{2}}$.
点评 解决本题的关键确定出甲车相对乙车的路程大小,结合相对速度进行求解,难度不大.

练习册系列答案
相关题目
15.关于磁感线的说法中正确的是( )
| A. | 磁感线都不是封闭曲线 | |
| B. | 磁感线都是封闭曲线 | |
| C. | 电流磁场的磁感线是封闭曲线,磁体的磁感线不是封闭曲线 | |
| D. | 电流磁场的磁感线不是封闭曲线,磁体的磁感线是封闭曲线 |
12.下列说法正确的是( )
| A. | 曲线运动可以是匀速运动,但是它一定是变速运动 | |
| B. | 平抛物体的加速度一定竖直向下,圆周运动的加速度一定指向圆心 | |
| C. | 做匀速圆周运动的物体,在任何相等的时间内通过的位移都相同 | |
| D. | 圆周运动的向心加速度方向始终与速度方向垂直 |
19.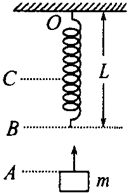 一个轻质弹簧,固定于天花板的O点处,原长为L,如图所示,一个质量为m的物块从A点竖直向上抛出,与弹簧在B点相接触,然后向上压缩弹簧,到C点时物块速度为零,在此过程中( )
一个轻质弹簧,固定于天花板的O点处,原长为L,如图所示,一个质量为m的物块从A点竖直向上抛出,与弹簧在B点相接触,然后向上压缩弹簧,到C点时物块速度为零,在此过程中( )
 一个轻质弹簧,固定于天花板的O点处,原长为L,如图所示,一个质量为m的物块从A点竖直向上抛出,与弹簧在B点相接触,然后向上压缩弹簧,到C点时物块速度为零,在此过程中( )
一个轻质弹簧,固定于天花板的O点处,原长为L,如图所示,一个质量为m的物块从A点竖直向上抛出,与弹簧在B点相接触,然后向上压缩弹簧,到C点时物块速度为零,在此过程中( )| A. | 由A到C的过程中,物块的机械能守恒 | |
| B. | 由A到B的过程中,物块的动能和重力势能之和变大 | |
| C. | 由B到C的过程中,弹性势能的变化量与克服弹力做的功相等 | |
| D. | 由A到C的过程中,重力势能的减少量等于弹性势能的增加量 |
16.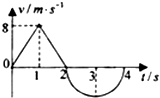 如图所示为某质点运动的v-t图象,2~4s内图线为半圆形,若4s末质点回到了出发点,则下列说法正确的是( )
如图所示为某质点运动的v-t图象,2~4s内图线为半圆形,若4s末质点回到了出发点,则下列说法正确的是( )
 如图所示为某质点运动的v-t图象,2~4s内图线为半圆形,若4s末质点回到了出发点,则下列说法正确的是( )
如图所示为某质点运动的v-t图象,2~4s内图线为半圆形,若4s末质点回到了出发点,则下列说法正确的是( )| A. | 1~2s内质点的加速度大小为8m/s2 | B. | 2~4s内质点的位移大小为8m | ||
| C. | 3s末质点的速度为8m/s | D. | 3s末质点的加速度等于零 |
15.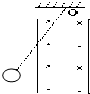 如图所示,一闭合金属圆环用绝缘细绳挂于O点,将圆环拉离平衡位置并释放,圆环摆动过程中经过匀强磁场区域,则(空气阻力不计)( )
如图所示,一闭合金属圆环用绝缘细绳挂于O点,将圆环拉离平衡位置并释放,圆环摆动过程中经过匀强磁场区域,则(空气阻力不计)( )
 如图所示,一闭合金属圆环用绝缘细绳挂于O点,将圆环拉离平衡位置并释放,圆环摆动过程中经过匀强磁场区域,则(空气阻力不计)( )
如图所示,一闭合金属圆环用绝缘细绳挂于O点,将圆环拉离平衡位置并释放,圆环摆动过程中经过匀强磁场区域,则(空气阻力不计)( )| A. | 圆环向右穿过磁场后,还能摆至原高度 | |
| B. | 在进入和离开磁场时,圆环中均有感应电流 | |
| C. | 圆环进入磁场后离最低点越近速度越大,感应电流也越大 | |
| D. | 圆环最终将静止在最低点 |
 如图所示,让摆球从图中的A位置由静止开始下摆,正好摆到最低点B位置时线恰好被拉断.设摆线长L=1.6m,摆球质量为0.5kg,悬点与地面的竖直高度为H=4.0m,不计空气阻力,g=10m/s2.求:
如图所示,让摆球从图中的A位置由静止开始下摆,正好摆到最低点B位置时线恰好被拉断.设摆线长L=1.6m,摆球质量为0.5kg,悬点与地面的竖直高度为H=4.0m,不计空气阻力,g=10m/s2.求: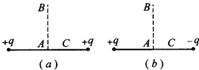 如图(a)中,A、B两点的场强大小相比EA<EB,A、B两点的电势高低相比φA>φB,图(b)中,A、C两点的场强大小相比EA<EC,A、C两点的电势高低相比φA>φC.(均选填“>”、“=”或“<”)
如图(a)中,A、B两点的场强大小相比EA<EB,A、B两点的电势高低相比φA>φB,图(b)中,A、C两点的场强大小相比EA<EC,A、C两点的电势高低相比φA>φC.(均选填“>”、“=”或“<”)