题目内容
17.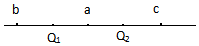 如图所示,Q1=2×10-12C,Q2=-4×10-12C,Q1、Q2相距12cm,求a、b、c三点的场强大小和方向,其中a为Q1、Q2的中点,b为Q1左方6cm处点,C为Q2右方6cm的点.
如图所示,Q1=2×10-12C,Q2=-4×10-12C,Q1、Q2相距12cm,求a、b、c三点的场强大小和方向,其中a为Q1、Q2的中点,b为Q1左方6cm处点,C为Q2右方6cm的点.
分析 根据点电荷场强公式E=k$\frac{Q}{{r}^{2}}$ 求出两个点电荷在a、b、c三点的电场强度大小,确定场强的方向,再根据电场的叠加原理求解.
解答 解:根据点电荷场强公式E=k$\frac{Q}{{r}^{2}}$ 得:
Q1在a点产生的场强大小为 E1a=9×109×$\frac{2×1{0}^{-12}}{0.0{6}^{2}}$=5N/C,方向向右.
Q1在b点产生的场强大小为 E1b=9×109×$\frac{2×1{0}^{-12}}{0.0{6}^{2}}$=5N/C,方向向左.
Q1在c点产生的场强大小为 E1c=9×109×$\frac{2×1{0}^{-12}}{0.1{8}^{2}}$=$\frac{5}{9}$N/C,方向向右.
Q2在a点产生的场强大小为 E2a=9×109×$\frac{4×1{0}^{-12}}{0.0{6}^{2}}$=10N/C,方向向右.
Q2在b点产生的场强大小为 E2b=9×109×$\frac{4×1{0}^{-12}}{0.1{8}^{2}}$=$\frac{10}{9}$N/C,方向向右.
Q2在c点产生的场强大小为 E2c=9×109×$\frac{4×1{0}^{-12}}{0.0{6}^{2}}$=10N/C,方向向左.
根据电场的叠加原理可得:a点的电场强度大小 Ea=E1a+E2a=15N/C,方向向右.
b点的电场强度大小 Eb=E1b-E2b=$\frac{35}{9}$ N/C,方向向左.
c点的电场强度大小 Ec=E2c-E1c=$\frac{85}{9}$ N/C,方向向左.
答:a点的电场强度大小为15N/C,方向向右.b点的电场强度大小为$\frac{35}{9}$N/C,方向向左.c点的电场强度大小为$\frac{85}{9}$N/C,方向向左.
点评 计算电场强度时,应先计算它的数值,电量的正负号不要代入公式中,然后根据场源电荷的电性判断场强的方向,用平行四边形法求得合矢量,就可以得出答案.

 阶梯计算系列答案
阶梯计算系列答案| A. | 甲向上、乙向上、丙向上 | B. | 甲向上、乙向上、丙不动 | ||
| C. | 甲向上、乙向上、丙向下 | D. | 甲向上、乙向下、丙不动 |
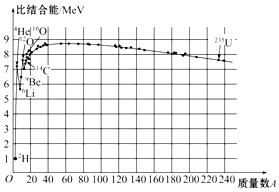
| A. | 重的原子核,例如,铀核(${\;}_{92}^{235}$U),因为它的核子多,核力大,所以结合得坚固而稳定 | |
| B. | 锂核(${\;}_{3}^{6}$Li)的核子的比结合能比铀核的比结合能小,因而比铀核结合得更坚固更稳定 | |
| C. | 原子核结合的松紧程度可以用“比结合能”来表征,比结合能的定义是每个核子的平均结合能;比结合能越大的原子核越稳定 | |
| D. | 以上三个表述都错误 |
| A. | 60m | B. | 50m | C. | 40m | D. | 30m |
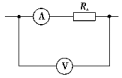 如图所示的电路中,电压表和电流表的读数分别为10V和0.1A,电流表的内阻为0.2Ω,则Rx的测量值100Ω;真实值99.8Ω.
如图所示的电路中,电压表和电流表的读数分别为10V和0.1A,电流表的内阻为0.2Ω,则Rx的测量值100Ω;真实值99.8Ω. 如图为某物体做直线运动的v-t图象.试分析物体在各段时间内的运动情况并计算各阶段加速度的大小和方向.
如图为某物体做直线运动的v-t图象.试分析物体在各段时间内的运动情况并计算各阶段加速度的大小和方向. 如图所示,在xOy平面内,以O1(0,R)为圆心、R为半径的圆形区域内有垂直平面向里的匀强磁场B1,x轴下方有一直线ab,ab与x轴相距为d,x轴与直线ab间区域有平行于y轴的匀强电场E,在ab的下方有一平行于x轴的感光板MN,ab与MN间区域有垂直于纸平面向外的匀强磁场B2.
如图所示,在xOy平面内,以O1(0,R)为圆心、R为半径的圆形区域内有垂直平面向里的匀强磁场B1,x轴下方有一直线ab,ab与x轴相距为d,x轴与直线ab间区域有平行于y轴的匀强电场E,在ab的下方有一平行于x轴的感光板MN,ab与MN间区域有垂直于纸平面向外的匀强磁场B2.