��Ŀ����
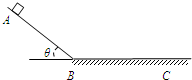 ��ͼ��ʾ������ӹ⻬б���ϵ�A���ɾ�ֹ��ʼ�»�������B������ֲ�ˮƽ�棨�辭��B��ǰ���ٶȴ�С���䣩�����ͣ��C�㣮ÿ��0.1sͨ���ٶȴ��������������˲ʱ�ٶȣ���������˲��ֲ������ݣ���g=10m/s2����
��ͼ��ʾ������ӹ⻬б���ϵ�A���ɾ�ֹ��ʼ�»�������B������ֲ�ˮƽ�棨�辭��B��ǰ���ٶȴ�С���䣩�����ͣ��C�㣮ÿ��0.1sͨ���ٶȴ��������������˲ʱ�ٶȣ���������˲��ֲ������ݣ���g=10m/s2����| t��s�� | 0.0 | 0.1 | 0.2 | �� | 0.8 | 0.9 | �� |
| v��m/s�� | 0.0 | 0.5 | 1.0 | �� | 1.2 | 1.0 | �� |
��2�������˶�����·�̣�
��������1�������ڹ⻬б�����»�ʱ�ļ��ٶ�a=gsin�ȣ����ݱ������������ֻҪ����»�ʱ�ļ��ٶȾͿ������б�����Ǧȣ�
��2�����������ȼ���ֱ���˶������ȼ���ֱ���˶��������ȼ����˶����ȼ����˶��ļ��ٶȣ���0.8sĩ��˲ʱ�ٶ���������˶�������ٶȣ��ٸ����ȼ��ٺ��ȼ����˶����ٶ�λ�ƹ�ϵ���λ�ƣ�
��2�����������ȼ���ֱ���˶������ȼ���ֱ���˶��������ȼ����˶����ȼ����˶��ļ��ٶȣ���0.8sĩ��˲ʱ�ٶ���������˶�������ٶȣ��ٸ����ȼ��ٺ��ȼ����˶����ٶ�λ�ƹ�ϵ���λ�ƣ�
�����14�֣���1����ǰ�������ݿ�֪������б�����ȼ����»�
�ɼ��ٶȹ�ʽa1=
��a1=5m/s2 ������
��ţ�ٵڶ�������mgsin��=ma1
�ɵã���=30��
��2���ɺ�������ݿ�֪������ˮƽ�����ȼ��ٻ���
�ɼ��ٶȹ�ʽa2=
��a2=2m/s2
����tʱ�������˶���B�㣬���ٶ����Ϊv������
v=a1t
����Ϊ��0.8 sʱ������ٶ�Ϊ1.2 m/s������
v=1.2+a2��0.8-t��
��֮��t=0.4s
v=2 m/s
��·��s=
+
=1.4 m
�𣺣�1��б�����Ǧ�=30��
��2�������˶�����·��Ϊ1.4m��
�ɼ��ٶȹ�ʽa1=
| ��v |
| ��t |
��ţ�ٵڶ�������mgsin��=ma1
�ɵã���=30��
��2���ɺ�������ݿ�֪������ˮƽ�����ȼ��ٻ���
�ɼ��ٶȹ�ʽa2=
| ��v |
| ��t |
����tʱ�������˶���B�㣬���ٶ����Ϊv������
v=a1t
����Ϊ��0.8 sʱ������ٶ�Ϊ1.2 m/s������
v=1.2+a2��0.8-t��
��֮��t=0.4s
v=2 m/s
��·��s=
| v2 |
| 2a1 |
| v2 |
| 2a2 |
�𣺣�1��б�����Ǧ�=30��
��2�������˶�����·��Ϊ1.4m��
��������ȷ���������ڹ⻬б���ϵ������Ӷ�����»�ʱ�ļ��ٶȣ������ȼ��ٺ��ȼ���ֱ���˶�����������ǹؼ���

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ��ʾ������ӹ⻬б���ϵ�A���ɾ�ֹ��ʼ�»�������B������ˮƽ�棨�辭��B��ǰ���ٶȴ�С���䣩�����ͣ��C�㣮ÿ��0.2sͨ���ٶȴ��������������˲ʱ�ٶȣ��±������˲��ֲ������ݣ����������ٶ�g=10m/s2����t=0.6sʱ��˲ʱ�ٶ�v��
��ͼ��ʾ������ӹ⻬б���ϵ�A���ɾ�ֹ��ʼ�»�������B������ˮƽ�棨�辭��B��ǰ���ٶȴ�С���䣩�����ͣ��C�㣮ÿ��0.2sͨ���ٶȴ��������������˲ʱ�ٶȣ��±������˲��ֲ������ݣ����������ٶ�g=10m/s2����t=0.6sʱ��˲ʱ�ٶ�v�� ��ͼ��ʾ������ӹ⻬б���ϵ�A���ɾ�ֹ��ʼ�»�������B������ˮƽ�棨�辭��B��ǰ���ٶȴ�С���䣩�����ͣ��C�㣮ÿ��0.2����ͨ���ٶȴ��������������˲ʱ�ٶȣ��±������˲��ֲ������ݣ����������ٶ�g=10m/s2��
��ͼ��ʾ������ӹ⻬б���ϵ�A���ɾ�ֹ��ʼ�»�������B������ˮƽ�棨�辭��B��ǰ���ٶȴ�С���䣩�����ͣ��C�㣮ÿ��0.2����ͨ���ٶȴ��������������˲ʱ�ٶȣ��±������˲��ֲ������ݣ����������ٶ�g=10m/s2�� ��ͼ��ʾ������ӹ⻬б���ϵ�A���ɾ�ֹ��ʼ�»�������B������ˮƽ�棨�辭��B��ǰ���ٶȴ�С���䣩�����ͣ��C�㣮ÿ��0.2����ͨ���ٶȴ��������������˲ʱ�ٶȣ��±������˲��ֲ������ݣ����������ٶ�g=10m/s2����
��ͼ��ʾ������ӹ⻬б���ϵ�A���ɾ�ֹ��ʼ�»�������B������ˮƽ�棨�辭��B��ǰ���ٶȴ�С���䣩�����ͣ��C�㣮ÿ��0.2����ͨ���ٶȴ��������������˲ʱ�ٶȣ��±������˲��ֲ������ݣ����������ٶ�g=10m/s2���� ��ͼ��ʾ������ӹ⻬б���ϵ�A���ɾ�ֹ��ʼ�»�������B������ˮƽ�棬���ͣ��C�㣮��ÿ��0.2sͨ������������������˶�����v���±������˲��ֲ������ݣ������徭��B��ǰ�����ʲ��䣬�������ٶ�gȡ10m/s2����
��ͼ��ʾ������ӹ⻬б���ϵ�A���ɾ�ֹ��ʼ�»�������B������ˮƽ�棬���ͣ��C�㣮��ÿ��0.2sͨ������������������˶�����v���±������˲��ֲ������ݣ������徭��B��ǰ�����ʲ��䣬�������ٶ�gȡ10m/s2����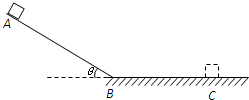 ��ͼ��ʾ������ӹ⻬б��Ķ���A���ɾ�ֹ��ʼ�ȼ����»�������B������ֲڵ�ˮƽ�����ȼ����˶����辭��B��ǰ���ٶȴ�С���䣩�����ͣ��C�㣮ÿ��0.2sͨ���ٶȴ���������������ٶȣ��±������˲��ֲ������ݣ�g=10m/s2����
��ͼ��ʾ������ӹ⻬б��Ķ���A���ɾ�ֹ��ʼ�ȼ����»�������B������ֲڵ�ˮƽ�����ȼ����˶����辭��B��ǰ���ٶȴ�С���䣩�����ͣ��C�㣮ÿ��0.2sͨ���ٶȴ���������������ٶȣ��±������˲��ֲ������ݣ�g=10m/s2����