题目内容
如图所示，物体从光滑斜面上的A点由静止开始下滑，经过B点后进入水平面（设经过B点前后速度大小不变），最后停在C点．每隔0.2秒钟通过速度传感器测量物体的瞬时速度，下表给出了部分测量数据．（重力加速度g=10m/s2）求：| t（s） | 0.0 | 0.2 | 0.4 | … | 1.2 | 1.4 | … |
| v（m/s） | 0.0 | 1.0 | 2.0 | … | 1.1 | 0.7 | … |
（2）物体与水平面之间的动摩擦因数μ；
（3）AB与BC的长度之比．
分析：（1）由表格读出物体在斜面上运动的速度与对应的时间，由加速度定义式求出加速度，再根据牛顿第二定律求解斜面的倾角α；
（2）研究物体由t=0到t=1.2s过程，根据斜面上匀加速运动的末速度等于水平面匀减速运动的初速度求物体在水平面匀减速时的加速度大小，然后根据牛顿第二定律列方程求动摩擦因数；
（3）根据速度位移公式列方程求AB与BC的长度之比．
（2）研究物体由t=0到t=1.2s过程，根据斜面上匀加速运动的末速度等于水平面匀减速运动的初速度求物体在水平面匀减速时的加速度大小，然后根据牛顿第二定律列方程求动摩擦因数；
（3）根据速度位移公式列方程求AB与BC的长度之比．
解答：解：（1）由前三列数据可知物体在斜面上匀加速下滑时的加速度为：
a1=
=
=5m/s2
根据牛顿第二定律得：mgsinα=ma1
代入数据解得：a=30°
（2）由后二列数据可知物体在水平面上匀减速滑行的加速度大小为：
a2=
=
=2m/s2
根据牛顿第二定律得：μmg=ma2
解得：μ=0.2
（3）设物体到达B点时速度为vB，由于斜面上匀加速运动的末速度等于水平面匀减速运动的初速度，则由匀变速直线运动规律得：
vB2=2a1xAB
vB2=2a2xBC
联立接的：
=
=
答：（1）斜面的倾角α为30°；（2）物体与水平面之间的动摩擦因数μ为0.2；（3）AB与BC的长度之比为2：5．
a1=
| △v |
| △t |
| 2.0-1.0 |
| 0.4-0.2 |
根据牛顿第二定律得：mgsinα=ma1
代入数据解得：a=30°
（2）由后二列数据可知物体在水平面上匀减速滑行的加速度大小为：
a2=
| △v |
| △t |
| 1.1-0.7 |
| 1.4-1.2 |
根据牛顿第二定律得：μmg=ma2
解得：μ=0.2
（3）设物体到达B点时速度为vB，由于斜面上匀加速运动的末速度等于水平面匀减速运动的初速度，则由匀变速直线运动规律得：
vB2=2a1xAB
vB2=2a2xBC
联立接的：
| xAB |
| xBC |
| a2 |
| a1 |
| 2 |
| 5 |
答：（1）斜面的倾角α为30°；（2）物体与水平面之间的动摩擦因数μ为0.2；（3）AB与BC的长度之比为2：5．
点评：本题由表格的形式反映物体的运动情况，运用运动学的基本公式求解加速度．要抓住物体在斜面上和水平面上运动之间速度关系，研究物体在斜面上运动的时间．
练习册系列答案
相关题目
如图所示，物体从光滑斜面上的A点由静止开始下滑，经过B点后进入水平面（设经过B点前后速度大小不变），最后停在C点．每隔0.2s通过速度传感器测量物体的瞬时速度，下表给出了部分测量数据．（重力加速度g=10m/s2）求：t=0.6s时的瞬时速度v．
如图所示，物体从光滑斜面上的A点由静止开始下滑，经过B点后进入水平面（设经过B点前后速度大小不变），最后停在C点．每隔0.2秒钟通过速度传感器测量物体的瞬时速度，下表给出了部分测量数据．（重力加速度g=10m/s2）
如图所示，物体从光滑斜面上的A点由静止开始下滑，经过B点后进入水平面，最后停在C点．现每隔0.2s通过传感器测量物体的运动速率v，下表给出了部分测量数据．设物体经过B点前后速率不变，重力加速度g取10m/s2．求：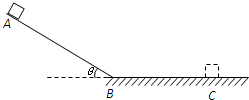
如图所示，物体从光滑斜面的顶端A点由静止开始匀加速下滑，经过B点后进入粗糙的水平面做匀减速运动（设经过B点前后速度大小不变），最后停在C点．每隔0.2s通过速度传感器测量物体的速度，下表给出了部分测量数据（g=10m/s2）．