题目内容
如图所示，物体从光滑斜面上的A点由静止开始下滑，经过B点后进入水平面，最后停在C点．现每隔0.2s通过传感器测量物体的运动速率v，下表给出了部分测量数据．设物体经过B点前后速率不变，重力加速度g取10m/s2．求：| t（s） | 0.0 | 0.2 | 0.4 | 0.6 | … | 1.4 | 1.6 | … |
| v（m/s） | 0.0 | 0.0 | 1.0 | 2.0 | … | 1.1 | 0.7 | … |
（2）物体与水平面之间的动摩擦因数μ
（3）物体运动到B点时的速率VB．
分析：（1）分析物体的运动过程，结合v-t测量数据，运用加速度定义式求出加速度大小；
（2）对物体在水平面上受力分析，运用牛顿第二定律求出问题．
（3）由表可知，物体开始运动的时刻t0=0.2s，设运动到B的时刻为t，根据运动学公式结合表格数据列式即可求解．
（2）对物体在水平面上受力分析，运用牛顿第二定律求出问题．
（3）由表可知，物体开始运动的时刻t0=0.2s，设运动到B的时刻为t，根据运动学公式结合表格数据列式即可求解．
解答：解：（1）根据题意知道物体先在斜面上做匀加速直线运动，然后在水平面上做匀减速直线运动到停止．
由公式a=
可得两段的加速度大小分别为：
a1=5m/s2，方向沿斜面向下；
a2=2m/s2，方向水平向左
（2）物体在水平面受重力、支持力、摩擦力．重力与支持力抵消，FN=mg，合力就是摩擦阻力．
根据牛顿第二定律
-μmg=ma2
代入数值得μ=0.2
（3）由表可知，物体开始运动的时刻t0=0.2s，设运动到B的时刻为t，则有如下运动学方程：
vB=a1（t-t0）
v1.4=vB+a2（t1.4-t）
由以上二式解得：t=0.7s，vB=2.5m/s
答：（1）物体在AB段和BC段的加度a1的大小为5m/s2，方向沿斜面向下，a2的大小为2m/s2，方向水平向左；
（2）物体与水平面之间的动摩擦因数为0.2；
（3）物体运动到B点时的速率VB为2.5m/s．
由公式a=
| △v |
| △t |
a1=5m/s2，方向沿斜面向下；
a2=2m/s2，方向水平向左
（2）物体在水平面受重力、支持力、摩擦力．重力与支持力抵消，FN=mg，合力就是摩擦阻力．
根据牛顿第二定律
-μmg=ma2
代入数值得μ=0.2
（3）由表可知，物体开始运动的时刻t0=0.2s，设运动到B的时刻为t，则有如下运动学方程：
vB=a1（t-t0）
v1.4=vB+a2（t1.4-t）
由以上二式解得：t=0.7s，vB=2.5m/s
答：（1）物体在AB段和BC段的加度a1的大小为5m/s2，方向沿斜面向下，a2的大小为2m/s2，方向水平向左；
（2）物体与水平面之间的动摩擦因数为0.2；
（3）物体运动到B点时的速率VB为2.5m/s．
点评：本题考查了牛顿第二定律及匀变速直线运动基本公式的应用，要求同学们能正确对物体进行受力分析．根据物理规律结合实验数据解决问题是考试中常见的问题．
练习册系列答案
寒假学与练系列答案
相关题目
如图所示，物体从光滑斜面上的A点由静止开始下滑，经过B点后进入水平面（设经过B点前后速度大小不变），最后停在C点．每隔0.2s通过速度传感器测量物体的瞬时速度，下表给出了部分测量数据．（重力加速度g=10m/s2）求：t=0.6s时的瞬时速度v．
如图所示，物体从光滑斜面上的A点由静止开始下滑，经过B点后进入水平面（设经过B点前后速度大小不变），最后停在C点．每隔0.2秒钟通过速度传感器测量物体的瞬时速度，下表给出了部分测量数据．（重力加速度g=10m/s2）
如图所示，物体从光滑斜面上的A点由静止开始下滑，经过B点后进入水平面（设经过B点前后速度大小不变），最后停在C点．每隔0.2秒钟通过速度传感器测量物体的瞬时速度，下表给出了部分测量数据．（重力加速度g=10m/s2）求：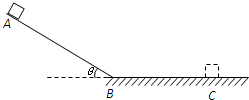
如图所示，物体从光滑斜面的顶端A点由静止开始匀加速下滑，经过B点后进入粗糙的水平面做匀减速运动（设经过B点前后速度大小不变），最后停在C点．每隔0.2s通过速度传感器测量物体的速度，下表给出了部分测量数据（g=10m/s2）．