题目内容
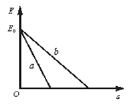
【题目】如图甲所示,MN、PQ是两根长为L=2m、倾斜放置的平行金属导轨,导轨间距d=1m,导轨所在平面与水平面成一定角度,M、P间接阻值为R=6Ω的电阻.质量为m=0.2kg、长度为d的金属棒ab放在两导轨上中点位置,金属棒恰好能静止.从t=0时刻开始,空间存在垂直导轨平面向上的匀强磁场,磁感应强度随时间变化如图乙所示,在t0=0.1s时刻,金属棒刚要沿导轨向上运动,此时磁感应强度B0=1.2T.已知金属棒与导轨始终垂直并且保持良好接触,不计金属棒和导轨电阻,设最大静摩擦力等于滑动摩擦力取重力加速度g=10m/s2.求：
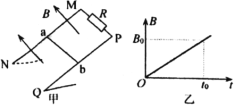
(1)0~t0时间内通过电阻R的电荷量q;
(2)金属棒与导轨之间的动摩擦因数u.
【答案】(1)0.2C (2) 0.75
【解析】
(1) (1)由题意得0~t0时间内回路中磁通量的变化量：
①
由法拉第电磁感应定律可得：
②
由欧姆定律可得：
③
故0~t0时间内通过电阻R的电荷量：q=IΔt ④
联立①②③④解得q=0.2C ；
(2) 由题意得导体棒在t=0时刻恰好能处于静止状态，设导轨平面与水平面之间的夹角为θ，
则有mgsinθ=fm ⑤
fm=μFN ⑥
FN=mgcosθ ⑦
在t0=0.1s时刻，金属棒刚要沿导轨向上运动，则有F安=mgsinθ+fm ⑧
此时F安=B0Id ⑨
联立⑤⑥⑦⑧⑨解得μ=0.75 .
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
