题目内容
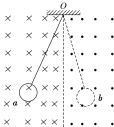
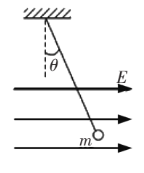
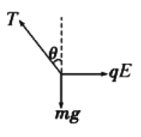
【题目】如图所示，在一足够大的空间内存在着水平向右的匀强电场，已知电场强度大小为E。有一质量为m的带电小球，用绝缘轻细线悬挂起来，静止时细线偏离竖直方向的夹角为
。重力加速度为g，不计空气阻力的作用。
（1）求小球所带的电荷量并判断所带电荷的性质；
（2）如果将细线轻轻剪断，细线剪断后，经过时间t，求这一段时间 内小球电势能的变化量。
【答案】（1）正电；
（2）
mg2t2（tan
）2
【解析】
（1）小球受到重力电场力F和细线的拉力T的作用，由共点力平衡条件有：
qE = Tsin.
mg = Tcos.
得：q= .
电场力的方向与电场强度的方向相同，故小球所带电荷为正电荷。
（2）剪断细线后，小球做匀加速直线运动，设其加速度为a，由牛顿第二定律有：
=ma
解得：a =
在t时间内，小球的位移为：l=at2 .
小球运动过程中，电场力做的功为：W= qElsin= mglsintan=mg2t2（tan）2
所以小球电势能的变化量（减少量）为：△Ep= mg2t2（tan）2
练习册系列答案
寒假学与练系列答案
相关题目
