题目内容
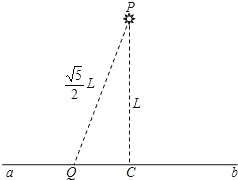
【题目】某游乐场的一项游乐设施如图甲所示,可以简化为如图乙所示的模型,已知圆盘的半径为R=2.5 m,悬绳长L=![]() R,圆盘启动后始终以恒定的角速度转动,圆盘先沿着杆匀加速上升,再匀减速上升直到到达最高点(整个上升过程比较缓慢),当圆盘上升到最高点转动时,悬绳与竖直方向的夹角为45°,重力加速度取g=10 m/s2。求:
R,圆盘启动后始终以恒定的角速度转动,圆盘先沿着杆匀加速上升,再匀减速上升直到到达最高点(整个上升过程比较缓慢),当圆盘上升到最高点转动时,悬绳与竖直方向的夹角为45°,重力加速度取g=10 m/s2。求:

(1)圆盘转动的角速度;
(2)若圆盘到达最高点时离地面的高度为h=22.5 m,为了防止乘客携带的物品意外掉落砸伤地面上的行人,地面上至少要设置多大面积的区域不能通行;
(3)已知甲乙两名乘客的质量分别是m1和m2(m1>m2),在圆盘加速上升的过程中,他们座椅上的悬绳与竖直方向的夹角分别为θ1和θ2,比较θ1和θ2的大小关系。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】(1)设乘客和座椅的总质量是m,悬绳拉力为FT
竖直方向上:FTcosθ=mg
水平方向上:FTsinθ=mω2(R+![]() Rsinθ)
Rsinθ)
以上两式联立解得ω=![]() rad/s。
rad/s。
(2)物品掉落时的速度v=ω(R+![]() Rsinθ)=5
Rsinθ)=5![]() m/s
m/s
物品掉落后做平抛运动
竖直方向有h-![]() Rcosθ=
Rcosθ=![]()
解得t=2 s
平抛运动的水平位移为x=vt=10![]() m
m
设置禁止通行区域半径为R′=![]() =15 m
=15 m
得S=πR′2=225π m2。
(3)设加速上升过程中,圆盘上升加速度为a
竖直方向:FTcosθ-mg=ma
水平方向:FTsinθ=mω2(R+![]() Rsinθ)
Rsinθ)
两式联立可得(g+a)tanθ=ω2(R+![]() Rsinθ)
Rsinθ)
可见θ与质量无关,即θ1=θ2。

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目