题目内容
（9分）如图所示，在光滑的水平地面上，质量为M=2kg的滑块上用轻杆及轻绳悬吊质量为m=lkg的小球，轻绳的长度为L=lm。此装置一起以速度v0=2m/s的速度向右滑动。另一质量也为M=2kg的滑块静止于上述装置的右侧。当两滑块相撞后，粘在一起向右运动，重力加速度为g=l0m/s2。求：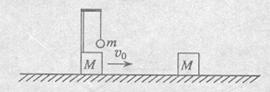
①两滑块粘在一起时的共同速度；
②小球向右摆动的最大高度。
①1 m/s ②0.04m
解析试题分析：①两滑块相撞过程，由于碰撞时间极短，小球的宏观位置还没有发生改变，两滑块已经达到共同速度，因此悬线仍保持竖直方向。由动量守恒定律，有Mv0＝2Mv（2分）
代入数据得：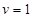
m/s（1分）
②两滑块碰撞完毕后，小球上升到最高点的过程，系统在水平方向上所受合外力为零，动量守恒，小球上升到最高点时，系统有相同的水平速度，则2Mv +mv0＝（2M+m）v′（2分）
解得，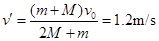
两滑块相撞后到小球上升到最高点，由能量守恒有：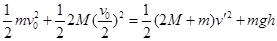
（2分）
代入数据得：
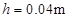（1分）
考点：动量守恒定律
练习册系列答案
相关题目
，
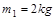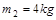的两个物体，其中
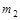左侧固定一轻质弹簧， 
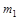以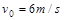
的速度向右运动，通过压缩弹簧与原来静止的
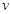= m/s，此时弹簧存储的弹性势能为__________J。
．已知木块与地面的动摩擦因素μ=
，重力加速度取g．求：
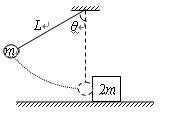
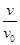的值 
