题目内容
如图所示，质量为m的小球悬挂在长为L的细线下端，将它拉至与竖直方向成θ=60°的位置后自由释放．当小球摆至最低点时，恰好与水平面上原来静止的、质量为2m的木块相碰，碰后小球速度反向且动能是碰前动能的
．已知木块与地面的动摩擦因素μ=
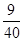，重力加速度取g．求：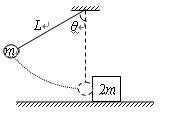
（1）小球与木块碰前瞬间所受拉力大小
（2）木块在水平地面上滑行的距离
（1）
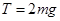（2）
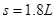
解析试题分析：（1）设小球摆至最低点时的速度为v，依动能定理有：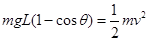
设小球与木块碰撞前瞬间所受拉力为T，有：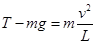 
代入数据，解得：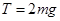
（2）设小球与木块碰撞后，小球的速度为v1，木块的速度为v2，设水平向右为正方向，依动量守恒定律有：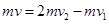
依题意知：
设木块在水平地面上滑行的距离为s，依动能定理有：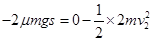
联立并代入数据，解得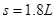
考点：动能定理 动量守恒定律
练习册系列答案
相关题目
如图，质量为m的人在质量为M的平板车上从左端走到右端，若不计平板车与地面的摩擦，则下列说法不正确的是（ ）
| A．人在车上行走时，车将向左运动 |
| B．当人停止走动时，由于车的惯性大，车将继续后退 |
| C．人以不同速度从车的左端走到右端，车在地面上移动的距离不变 |
| D．不管人在车上行走的速度多大，车在地面上移动的距离都相同 |
