如图所示.光滑水平面上一质量为M.长为L的木板右端靠竖直墙壁.质量为m的小滑块以水平速度v0滑上木板的左端.滑到木板的右端时速度恰好为零.①求小滑块与木板间的摩擦力大小,②现小滑块以某一速度v滑上木板的左端.滑到木板的右端时与竖直墙壁发生弹性碰撞.然后向左运动.刚好能够滑到时木板左端而不从木板上落下.试求的值题目和参考答案——青夏教育精英家教网—

题目内容

（9分）如图所示，光滑水平面上一质量为M、长为L的木板右端靠竖直墙壁。质量为m的小滑块（可视为质点）以水平速度v₀滑上木板的左端，滑到木板的右端时速度恰好为零。

①求小滑块与木板间的摩擦力大小；
②现小滑块以某一速度v滑上木板的左端，滑到木板的右端时与竖直墙壁发生弹性碰撞，然后向左运动，刚好能够滑到时木板左端而不从木板上落下，试求的值

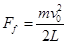① ；②

解析试题分析：①小滑块以水平速度v₀右滑时，有：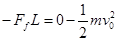
         2分
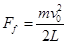解得             1分
②小滑块以速度v滑上木板到运动至碰墙时速度为v₁，则有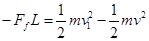
          1分
滑块与墙碰后至向左运动到木板左端，此时滑块、木板的共同速度为v₂，则有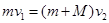
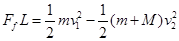                  2分
           2分
上述四式联立，解得           1分
考点：考查学生综合应用动量守恒定律和能量守恒定律在碰撞问题中的应用能力．

练习册系列答案

相关题目

牛顿的《自然哲学的数学原理》中记载，A、B两个玻璃球相碰，碰撞后的分离速度和它们碰撞前的接近速度之比总是约为15∶16。分离速度是指碰撞后B对A的速度，接近速度是指碰撞前A对B的速度。若上述过程是质量为2m的玻璃球A以速度v₀碰撞质量为m的静止玻璃球B，且为对心碰撞，求碰撞后A、B的速度大小。

如图所示，光滑的水平面上有m_A=2kg，m_B= m_C=1kg的三个物体，用轻弹簧将A与B连接．在A、C两边用力使三个物体靠近，A、B间的弹簧被压缩，此过程外力做功72 J，然后从静止开始释放，求当物体B与C分离时，B对C做的功有多少？

（9分）如图所示，在光滑的水平地面上，质量为M=2kg的滑块上用轻杆及轻绳悬吊质量为m=lkg的小球，轻绳的长度为L=lm。此装置一起以速度v₀=2m/s的速度向右滑动。另一质量也为M=2kg的滑块静止于上述装置的右侧。当两滑块相撞后，粘在一起向右运动，重力加速度为g=l0m/s²。求：

①两滑块粘在一起时的共同速度；
②小球向右摆动的最大高度。

(9分）如图所示，在光滑的水平面上，有一质量为M="3" kg的薄板和质量m=1kg的物块。现给薄板和物块相同的初速度v=4m/s朝相反方向运动，它们之间有摩擦，薄板足够长，求

①当薄板的速度为2.4m/s时，物块的速度大小和方向。
②薄板和物块最终停止相对运动时，因摩擦而产生的热量。

（13分）如图所示，在光滑的水平面上有一长为L的木板B，上表面粗糙，在其左端有一光滑的1/4圆弧槽C，与长木板接触但不相连，圆弧槽的下端与木板上表面相平，B、C静止在水平面上。现有滑块A以初速v₀从右端滑上B，一段时间后，以v₀/2滑离B，并恰好能到达C的最高点。A、B、C的质量均为m。求：

⑴A刚滑离木板B时，木板B的速度；
⑵A与B的上表面间的动摩擦因数μ；
⑶圆弧槽C的半径R；
⑷从开始滑上B到最后滑离C的过程中A损失的机械能。

如图所示，A、B两球放在光滑的水平面上，水平面的右侧与竖直平面内一光滑曲面相切，现给A一向右的速度，让A与B发生对心弹性碰撞，小球沿曲面上升到最高点后又能再沿曲面滑回到水平面。若要B返回水平面时能再与么发生碰撞， A、B的质量应满足什么关系？

一列简谐横波沿直线传播的速度是2m/s，在传播方向上有A、B两点，从波刚好传到某质点时开始计时，已知5s内A点完成了6次全振动，B点完成了10次全振动，则此波的传播方向为（填“A→B”或“B→A”），波长为，A、B两点间的距离为 m。

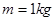（7分）如图所示，在水平光滑直导轨上，静止着三个质量均为的相同小球A、B、C。现让A球以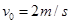的速度向B球运动，A、B两球碰撞后粘合在一起，两球继续向右运动并跟C球碰撞，碰后C球的速度。求：

（1）A、B两球碰撞后瞬间的共同速度；
（2）两次碰撞过程中损失的总动能。

试题分类