题目内容
17. 在光滑水平而上放着质量分别为m和2m的AB两个物块,两物块间用一轻弹簧拴接在一起;现用外力缓慢向左推B物块使弹簧压缩,此过程中推力做功W,然后撤去外力,则:( )
在光滑水平而上放着质量分别为m和2m的AB两个物块,两物块间用一轻弹簧拴接在一起;现用外力缓慢向左推B物块使弹簧压缩,此过程中推力做功W,然后撤去外力,则:( )| A. | 从撤去外力到A离开墙面的过程中,A、B两个物块的总动量守恒 | |
| B. | 当A离开墙面时,B的动量大小为$\sqrt{2mW}$ | |
| C. | A离开墙面后,当A、B相距最远时弹黄的弹性势能为$\frac{1}{3}$W | |
| D. | A离开墙面后,当A的动量最大时弹簧形变量为零 |
分析 根据冲量的定义判断系统的动量是否守恒;撤去力F后,B向右运动,弹簧弹力逐渐减小,当弹簧恢复原长时,A开始脱离墙面,这一过程机械能守恒.
A离开墙壁后系统机械能守恒动量也守恒,故系统动能不可以为0,则弹簧弹性势能不可能与系统总机械能相等.
解答 解:A、从撤去外力到A离开墙面的过程中,A、B两个物块组成的系统始终受到墙壁的向右支持力,总动量不守恒,故A错误
B、撤去力F后,B向右运动,弹簧弹力逐渐减小,当弹簧恢复原长时,A开始脱离墙面,这一过程机械能守恒,即满足:
W=E=$\frac{1}{2}$(2m)vB2
vB=$\sqrt{\frac{W}{m}}$
B的动量大小为2$\sqrt{mW}$,故B错误
C、撤去F后,A离开竖直墙后,当两物体速度相同时,弹簧伸长最长或压缩最短,弹性势能最大.
设两物体相同速度为v,A离开墙时,B的速度为v0.根据动量守恒和机械能守恒得
2mvB=3mv,
W=$\frac{1}{2}$•3mv2+EP
又W=$\frac{1}{2}$×2m${v}_{B}^{2}$
联立得到,v=$\frac{2}{3}\sqrt{\frac{W}{m}}$
弹簧的弹性势能最大值为EP=$\frac{W}{3}$.故C正确
D、A离开墙面时B的速度大,A的速度等于0,所以弹簧被拉长,A开始做加速运动,B做减速运动,当二者的速度相同时,弹簧最长;然后弹簧开始收缩,A的速度继续增大,B的速度继续减小,当弹簧恢复原长时,A的速度达到最大,所以当A的动量最大时弹簧形变量为零.故D正确
故选:CD
点评 正确认识动量守恒条件和机械能守恒条件是解决本题的关键了.如果一个系统不受外力或所受外力的矢量和为零,那么这个系统的总动量保持不变,这个结论叫做;系统只有重力或弹力做功为机械能守恒条件.

 阅读快车系列答案
阅读快车系列答案 如图,粗糙水平面上a、b、c、d四个相同小物块用四根完全相同的轻弹簧连接,正好组成一个等腰梯形,系统静止,ab之间、ac之间以及bd之间的弹簧长度相同且等于cd之间弹簧长度的一半,ab之间弹簧弹力大小为cd之间弹簧弹力大小的一半,若a受到的摩擦力大小为f,则下列说法不正确的是( )
如图,粗糙水平面上a、b、c、d四个相同小物块用四根完全相同的轻弹簧连接,正好组成一个等腰梯形,系统静止,ab之间、ac之间以及bd之间的弹簧长度相同且等于cd之间弹簧长度的一半,ab之间弹簧弹力大小为cd之间弹簧弹力大小的一半,若a受到的摩擦力大小为f,则下列说法不正确的是( )| A. | ab之间的弹簧一定是压缩的 | B. | b受到的摩擦力大小为f | ||
| C. | d受到的摩擦力大小为2f | D. | c受到的摩擦力大小为$\sqrt{3}$f |
| A. | $\frac{1}{3}$v | B. | $\frac{2}{3}$v | C. | $\frac{2}{9}$v | D. | $\frac{4}{9}$v |
 铁路弯道处内外轨道高度是不同的,已知内外轨道平面与水平面的倾角为θ,转弯处的弯道半径为R,如图所示,若质量为m的火车转弯时速度小于$\sqrt{gRtanθ}$,则( )
铁路弯道处内外轨道高度是不同的,已知内外轨道平面与水平面的倾角为θ,转弯处的弯道半径为R,如图所示,若质量为m的火车转弯时速度小于$\sqrt{gRtanθ}$,则( )| A. | 外轨对外侧车轮有挤压 | |
| B. | 内轨对内侧车轮有挤压 | |
| C. | 这时铁轨对火车垂直于轨道平面的支持力小于$\frac{mg}{cosθ}$ | |
| D. | 这时铁轨对火车垂直于轨道平面的支持力等于$\frac{mg}{cosθ}$ |
| A. | 物体的动量越大,说明它的惯性越大 | |
| B. | 物体的动量变化越快,说明它所受合力的冲量越大 | |
| C. | 物体的动量发生变化,它的动能不一定发生变化 | |
| D. | 物体的加速度不变,它的动量一定不变 |
| A. | 气球匀速下降 | B. | 气球匀速上升 | C. | 气球加速上升 | D. | 气球加速下降 |
 如图所示,地面上竖立着一轻质弹簧,小球从其正上方某一高度处自由下落到弹簧上.从小球接触弹簧到将弹簧压缩至最短的过程中(弹簧一直保持竖直)( )
如图所示,地面上竖立着一轻质弹簧,小球从其正上方某一高度处自由下落到弹簧上.从小球接触弹簧到将弹簧压缩至最短的过程中(弹簧一直保持竖直)( )| A. | 小球动能一直减小 | |
| B. | 小球的重力势能先增大后减小 | |
| C. | 小球和弹簧及地球组成的系统总机械能守恒 | |
| D. | 小球重力势能与弹簧弹性势能之和先减小后增加 |
| A. | 轨道半径越大线速度越小 | B. | 轨道半径越大向心加速度越大 | ||
| C. | 轨道半径越大周期越大 | D. | 轨道半径越大周期越小 |
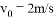 开始从斜面顶端匀加速下滑,第4s末的速度为6m/s,求:
开始从斜面顶端匀加速下滑,第4s末的速度为6m/s,求: