Question

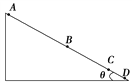
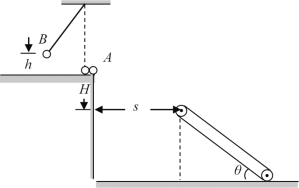
【题目】如图所示，在台阶的水平台面边缘静止一质量为m=0.1kg的小球A，在紧靠A的左侧用细线竖直挂一同样大小的小球B，两球心连线水平。在平台下面的地面上有一倾角为θ=37°的传送带，传送带顺时针转动，长度为，传送带的上端离台阶的高度H=0.45m。把小球B拉到离平台h=0.8m高处由静止释放，与小球A正碰后B的速率变为碰撞前的，小球A恰好沿平行于传送带的方向从传送带的上端飞上传送带并沿传送带运动。已知小球A与传送带之间的动摩擦因数为，重力加速度为g=10m/s2。求：

（1）传送带上端与台阶的水平距离s；

（2）求小球B的质量；

（3）若要使小球A能在最短时间内到达传送带底端，传送带转动的速度应满足什么条件？

Answer 1

【答案】（1）；（2）；（3）传送带的速度应该满足：

【解析】

（1）小球A做平抛运动，有：

到达传送带上端时，竖直方向：

传送带上端与台阶的水平距离：

解得：

（2）设B与A碰前的速度为，由动能定理，得：

解得：

碰后B的速度大小为：

若碰后B的速度水平向右，由能量守恒定律，得：

解得：

因，故此情况成立。

若碰后B的速度水平向左，则

解得：

因，故此情况不成立。

（3）设小球A在传送带运动时的最大速度为，由牛顿第二定律得：

解得

设传送带速度为V时，小球A恰能以一直匀加速至传送带下端并与传送带共速。

小球A滑上传送带的速度：

由运动学公式，得：

解得：

故传送带的速度应该满足：