��Ŀ����
����Ŀ����ͼ��ʾ�����Ϊ����б������A��B��C���㣬�ִ�������ֱ��Բ�ͬ�ij��ٶ�ˮƽ�׳�һС������С�������б���ϵ�D�㣬����AB��BC��CD��5��3��1�ɴ˿��ж�(����)
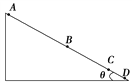
A. ABC������С���˶�ʱ��֮��Ϊ1��2��3
B. A��B��C������С������б����ʱ�ٶ�����ٶȼ�ļн�֮��Ϊ1��1��1
C. A��B��C������С��ij��ٶȴ�С֮��Ϊ3��2��1
D. A��B��C������С����˶��켣�����ڿ����ཻ
���𰸡�BC
�����������ݼ��ι�ϵ�ɵ�����С������ĸ߶�֮��Ϊ��9��4��1����![]() ���ɵ÷���ʱ��֮��Ϊ��3��2��1����A������Ϊ����С��λ�Ƶķ�����ͬ���ٶȼн�����ֵһ����λ�Ƽн�����ֵ��2���������ٶ�����ٶ�֮��ļн�һ����ȣ���Ϊ1��1��1����B��ȷ��������С�������ˮƽλ��֮��Ϊ��9��4��1��ʱ��֮��Ϊ��3��2��1��ˮƽ������x=vt�ɵã����ٶȴ�С֮��Ϊ��3��2��1����C��ȷ��������������䵽ͬһ�㣬������С����˶��������ڿ����ཻ����D��������BC��ȷ��AD������
���ɵ÷���ʱ��֮��Ϊ��3��2��1����A������Ϊ����С��λ�Ƶķ�����ͬ���ٶȼн�����ֵһ����λ�Ƽн�����ֵ��2���������ٶ�����ٶ�֮��ļн�һ����ȣ���Ϊ1��1��1����B��ȷ��������С�������ˮƽλ��֮��Ϊ��9��4��1��ʱ��֮��Ϊ��3��2��1��ˮƽ������x=vt�ɵã����ٶȴ�С֮��Ϊ��3��2��1����C��ȷ��������������䵽ͬһ�㣬������С����˶��������ڿ����ཻ����D��������BC��ȷ��AD������

��ϰ��ϵ�д�
�����Ŀ