题目内容
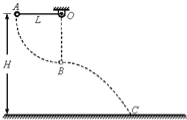
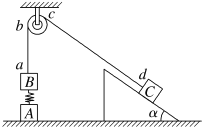
【题目】如图所示，在竖直方向上A、B两物体通过劲度系数为k的轻质弹簧相连，A放在水平地面上，B、C两物体通过细线绕过轻质定滑轮相连，C放在固定的光滑斜面上．用手拿住C，使细线刚刚拉直但无拉力作用，并保证ab段的细线竖直、cd段的细线与斜面平行．已知A、B的质量均为m，C的质量为4m，重力加速度为g，细线与滑轮之间的摩擦不计，开始时整个系统处于静止状态，释放C后C沿斜面下滑，A刚离开地面时，B获得最大速度．求：
(1)斜面倾角α；
(2)B的最大速度v.
【答案】(1)30°(2)2g
【解析】
(1)当物体A刚离开地面时，设弹簧的伸长量为xA，对A有
；
此时B受到重力
、弹簧的弹力
、细线拉力FT三个力的作用，设B的加速度为a，根据牛顿第二定律，对B有：
，
对C有：
，
当B获得最大速度时，有
，由此解得
，所以
(2)开始时弹簧压缩的长度为
，显然
当物体A刚离开地面时，B上升的距离以及C沿斜面下滑的距离均为
由于
，弹簧处于压缩状态和伸长状态时的弹性势能相等，而且物体A刚离开地面时，B、C两物体的速度相等，设为v，
由机械能守恒定律得
，
代入数值解得
.
练习册系列答案
相关题目
