题目内容
【题目】如图所示，ad、bd、cd 是竖直面内三根固定的光滑细杆，a、b、c、d 位于同一圆周上，a 点为圆周的最高点，d 点为最低点。每根杆上都套着一个质量相同的小滑环(图中未画出)，三个滑环分别从a、b、c 处无初速度释放，下列说法正确的是（ ）
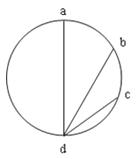
A.三个环受到的重力冲量相等
B.沿 bd 杆运动的环受到的支持力冲量最大
C.三个环的动量增量相同
D.沿 cd 杆运动的环受到的支持力冲量最大
【答案】AD
【解析】
设任一细杆与竖直方向的夹角为α，环运动的时间为t，圆周的直径为D．则环的加速度大小
a=gcosα
由位移公式得：
得到
所以三个环运动时间相同。
A．由于三个环的重力相等，运动时间相同，由公式I=Ft分析可知，各环重力的冲量相等。故A正确；
BD．c环受到的支持力最大，运动时间相等，则支持力对环c的冲量最大。故B错误，D正确；
C．a环的加速度最大，受到的合力最大，则合力对a环的冲量最大，根据动量定理可知，动量增量最大，故C错误。
练习册系列答案
考前必练系列答案
相关题目
