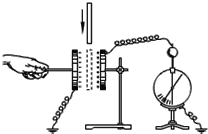
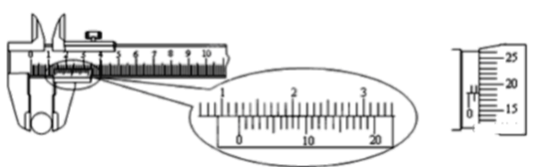
��Ŀ����
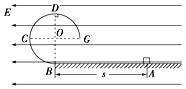
����Ŀ������ͼ��ʾ�Ŀռ������y������һ��ǿ�糡����ǿ�����y���������600����СΪE=4.0��105N/C��y���ҷ���һ��ֱֽ���������ǿ�ų����Ÿ�Ӧǿ��B=0.20T.��һ�������ٶ�v=2.0��106m/s����x���ϵ�A��(10cm��0)����x���������300б��������ų����ڴų����˶�һ��ʱ�������糡�����ֻص��ų������ų����ú�������糡.��֪������������Ϊm=1.6��10-27kg�����q=1.6��10-19C��������������.��:(����������3λ��Ч����)
��1�������ڴų�����Բ���˶��İ뾶.
��2�����Ӵӿ�ʼ�˶����ڶ��ε���y����������ʱ��.
��3�����ӵ����ε���y���λ������.

���𰸡�(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
��������(1)�����ڴų�������������������Բ���˶���������������Բ���˶��İ뾶ΪR���������������ṩ�������� ![]()
��ã� ![]() ��
��
(2)�������ӵij��ٶȷ�����x��������н�Ϊ30���Ұ뾶ǡ�õ���OA����ˣ����ӽ��ڴų��������Բ�ܵ���y���ϵ�C�㣬��ͼ��ʾ��
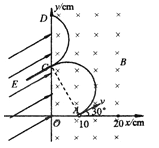
������Բ���˶�����Ϊ�� ![]() ��
��
���Ӵӳ����˶�����һ�ε���y���ʱ��Ϊ�� ![]() ��
��
�����ڵ糡���������������ļ��ٶȣ� ![]()
�����ڵ糡�������˶���ʱ��t2�����У�t2=2v/a=��2��2��106��/(4��10-13)s=1��10-7s��
������Ӵӿ�ʼ�˶����ڶ��ε���y����������ʱ�䣺
t=t1+t2=1.57��10-7s+1��10-7s= ![]() s��
s��
(3)�����ٴν���ų�ʱ���ٶȵķ�����糡�ķ�����ͬ��������������������������Բ���˶�������y���D�㡣
���ݼ��ι�ϵ,���Եó�C�㵽D��ľ���Ϊ��CD=2Rcos30��
�����ӵڶ��ε���y���λ��Ϊ��
y2=CD+OC=2Rcos30+2Rcos30=20![]() cm��34.6cm��
cm��34.6cm��
�����ӵ����ε���y�������Ϊ(0,34.6cm).