��Ŀ����
����Ŀ����ͼ����ʾ����һ��ľ�徲ֹ���㹻���Ĵֲ�ˮƽ���ϣ�ľ������ΪM=4kg����ΪL=1.4m��ľ���Ҷ˷ŵ�һС���飬С��������Ϊm=1kg������Ϊ�ʵ㣮����ˮƽ����F������ľ��M�Ҷˣ�����Fȡ��ͬ��ֵʱ��С�����ľ��ļ��ٶȷֱ��Ӧ��ͬ��ֵ�����ߵ�a��Fͼ����ͼ����ʾ��ȡg=10m/s2 �� ��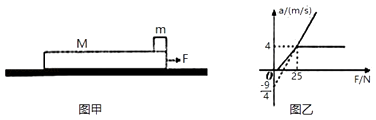
��1��С������ľ��֮��Ļ���Ħ���������Լ�ľ�������Ļ���Ħ��������
��2����ˮƽ����F=27.8N����ʼ��������ľ��M�ϣ���С����m��ľ���ϻ���ʱ��������ʱ��Ϊ�
���𰸡�
��1��
�⣺��ͼ�ҿ�֪��������F��25Nʱ��С������ľ�彫������Ի�������С����Ϊ�о�������ţ�ٵڶ����ɵ�
��1mg=ma1
��ͼ֪��a1=4m/s2
�������ݽ�� ��1=0.4
��ľ��Ϊ�о�������ţ�ٵڶ������У�
F����1mg����2��m+M��g=Ma2
��� a2= ![]() F��
F�� ![]()
���ͼ��ɵã��� ![]() =��
=�� ![]()
�������ݽ�� ��2=0.1
��2��
�⣺��m��M�ϻ�����ʱ��Ϊt����ˮƽ����F=27.8Nʱ��
�ɣ�1��֪����ļ��ٶ�Ϊ a1=��1g=4m/s2
��������ʱ��t�ڵ�λ��Ϊ s1= ![]() a1t2��
a1t2��
�ɣ�1����֪ľ��ļ��ٶ�Ϊ a2= ![]()
�������ݽ�� a2=4.7m/s2
��ľ����ʱ��t�ڵ�λ��Ϊ s2= ![]() a2t2��
a2t2��
�����֪��s1��s2=L
��������������� t=2s
����������1����ͼ��֪��������F��25Nʱ��С������ľ�彫������Ի���������ļ��ٶȣ����ţ�ٵڶ��������������ľ���Ķ�Ħ����������ľ���о�������ţ�ٵڶ����ɵó����ٶȵı���ʽ�����ͼ�����ľ��������Ķ�Ħ����������2������ţ�ٵڶ����ɷֱ�ó������ľ��ļ��ٶȣ�����λ��֮�����L������˶�ѧ��ʽ���������ʱ�䣮

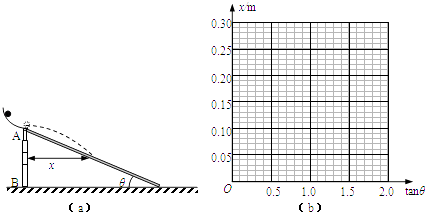
����Ŀ����ͼ��ʾ��AB��һ����������ֱ֧�ܣ�֧�ܶ���A���̶�һ���ι�������ĩ��ˮƽ��һ����ľ����϶˽½��ڹ�A��ˮƽת���ϣ��¶˸���ˮƽ�����ϣ���һС��ӻ����ijһλ���ɾ�ֹ�ͷţ�С������ľ���ϵ�ij�������С��ƽ���˶���ˮƽ���x�ʹ�ʱľ����ˮƽ��ļнǦȣ������tan�ȣ��ı�֧��AB�ĸ߶ȣ���С���ͬһλ���ͷţ��ظ�ʵ�飬�õ�����x��tan�ȣ���¼�����������
ʵ����� | 1 | 2 | 3 | 4 | 5 | 6 |
tan�� | 0.18 | 0.32 | 0.69 | 1.00 | 1.19 | 1.43 |
x/m | 0.035 | 0.065 | 0.140 | 0.160 | 0.240 | 0.290 |
��1����ͼ��b����������������ߣ�����x��tan�ȵĹ�ϵͼ��
��2������x��tan��ͼ���֪С����ƽ���˶��ij��ٶ�v0=m/s��ʵ���з��֦ȳ���60���С���������б���ϣ���б��ij���Ϊ m�����������ٶ�gȡ10m/s2����
��3��ʵ������һ�����ݳ������Դ����ܵ�ԭ���� ��