题目内容
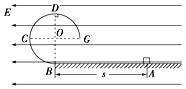
【题目】如图所示,BCDG是光滑绝缘的![]() 圆形轨道,位于竖直平面内,轨道半径为R,下端与水平绝缘轨道在B点平滑连接,整个轨道处在水平向左的匀强电场中.现有一质量为m、带正电的小滑块(可视为质点)置于水平轨道上,滑块受到的电场力大小为
圆形轨道,位于竖直平面内,轨道半径为R,下端与水平绝缘轨道在B点平滑连接,整个轨道处在水平向左的匀强电场中.现有一质量为m、带正电的小滑块(可视为质点)置于水平轨道上,滑块受到的电场力大小为
![]() mg,滑块与水平轨道间的动摩擦因数为0.5,重力加速度为g.
mg,滑块与水平轨道间的动摩擦因数为0.5,重力加速度为g.
(1)若滑块从水平轨道上距离B点s=3R的A点由静止释放,滑块到B点时速度为多大?
(2)求滑块到达C点时受到轨道的作用力大小;
(3)改变s的大小,使滑块恰好始终沿轨道滑行,且从G点飞出轨道,求滑块在圆轨道上滑行过程中的最小速度大小.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】 (1)设滑块到达B点时的速度为v,滑块从A到B的过程,由动能定理有: ![]()
而![]()
解得![]() ;
;
(2)设滑块到达C点时的速度为vC,滑块从A到C的过程,由动能定理有:
![]()
设滑块到达C点时受到轨道的作用力大小为F,则
由牛顿第二定律得: ![]()
解得: ![]()
(3)要使滑块恰好始终沿轨道滑行,则滑至圆轨道DG间某点,由电场力和重力的合力提供向心力,此时的速度最小(设为vn),则有
![]()
解得: ![]()

 全能测控期末小状元系列答案
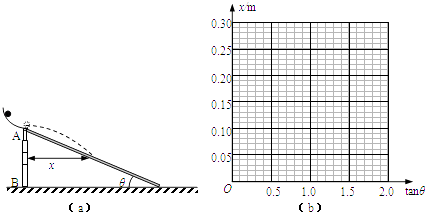
全能测控期末小状元系列答案【题目】如图所示,AB是一可升降的竖直支架,支架顶端A处固定一弧形轨道,轨道末端水平.一条形木板的上端铰接于过A的水平转轴上,下端搁在水平地面上.将一小球从弧型轨道某一位置由静止释放,小球落在木板上的某处,测出小球平抛运动的水平射程x和此时木板与水平面的夹角θ,并算出tanθ.改变支架AB的高度,将小球从同一位置释放,重复实验,得到多组x和tanθ,记录的数据如表:
实验次数 | 1 | 2 | 3 | 4 | 5 | 6 |
tanθ | 0.18 | 0.32 | 0.69 | 1.00 | 1.19 | 1.43 |
x/m | 0.035 | 0.065 | 0.140 | 0.160 | 0.240 | 0.290 |
(1)在图(b)的坐标中描点连线,做出x﹣tanθ的关系图象;
(2)根据x﹣tanθ图象可知小球做平抛运动的初速度v0=m/s;实验中发现θ超过60°后,小球将不会掉落在斜面上,则斜面的长度为 m.(重力加速度g取10m/s2);
(3)实验中有一组数据出现明显错误,可能的原因是 .