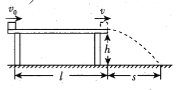
题目内容
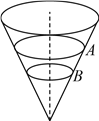
【题目】如图所示，两个靠静摩擦力传动的轮子，大轮半径是小轮半径的2倍，大轮中C点离圆心O2的距离等于小轮半径，A、B分别为两个轮边缘上的点，则A、B、C三点的（ ）
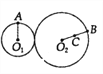
A. 线速度之比为2：2：1 B. 角速度之比为2：1：1
C. 向心加速度之比为4：2：1 D. 转动周期之比为2：1：1
【答案】ABC
【解析】A项：两个靠静摩擦力传动，所以两轮边缘线速相同，即
，B、C两点属同轴转动即角速度相同，所以
，故三者线速度之比为
，故A正确；
B项：B、C两点属同轴转动角速度相同，即
，由于
，所以
，所以角速度之比为
，故B正确；
C项：根据公式
可得， 
，根据公式
可得， 
，所以向心加速度之比为
，故C正确；
D项：根据公式可得， 
，根据公式
得， 
，所以周期之比为1：2：2，故D错误。
点晴：解决本题的关键知道靠传送带传动轮子边缘上的点具有相同的线速度，共轴转动的点，具有相同的角速度。
练习册系列答案
学业测评一课一测系列答案
相关题目
