题目内容
20.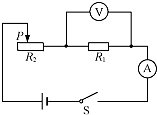 如图所示,电源电压保持6V 不变,电流表的量程为0~0.6A,电压表的量程为0~3V,定值电阻R1的规格为“10Ω 0.5A”,滑动变阻器R2 的规格为“20Ω 1A”.闭合开关,为了保证电路安全,在变阻器滑片P 移动过程中,下列说法正确的是( )
如图所示,电源电压保持6V 不变,电流表的量程为0~0.6A,电压表的量程为0~3V,定值电阻R1的规格为“10Ω 0.5A”,滑动变阻器R2 的规格为“20Ω 1A”.闭合开关,为了保证电路安全,在变阻器滑片P 移动过程中,下列说法正确的是( )| A. | 电阻R1 消耗功率允许的变化范围为0.4W~0.9W | |
| B. | 电流表示数允许的变化范围为0.2A~0.5A | |
| C. | 变阻器R2接入电路的阻值允许变化范围为2Ω~20Ω | |
| D. | 电路消耗总功率允许的变化范围为1.2W~3W |
分析 滑动变阻器${R}_{2}^{\;}$与定值电阻${R}_{1}^{\;}$串联,电压表测量定值电阻两端的电压,根据串联电路的分压原理(电阻越大,电阻两端的电压越高),当电压表的示数最小时,变阻器接入电路的电阻最大;当电流表的示数达到最大值时,变阻器接入电路的电阻最小;根据欧姆定律的应用可分别求电路中的总电阻和滑动变阻器接入电路中的电阻值,同时可以确定电压表示数、电流表示数以及电路中总功率的变化.
解答 解:电源两端电压为6V保持不变,定值电阻为10Ω;
由题意知,当电压表的最大测量值为3V时,此时定值电阻${R}_{1}^{\;}$两端的电压为:${U}_{1}^{\;}=3V$,电路中的电流为:${I}_{1}^{\;}=I={I}_{2}^{\;}=\frac{{U}_{1}^{\;}}{{R}_{1}^{\;}}=\frac{3V}{10Ω}=0.3A<0.6A$,因此电路中的最大电流为0.3A;
故滑动变阻器接入电路中的最小电阻为:${R}_{2}^{\;}=\frac{6V-3V}{0.3A}=10Ω$;电路消耗的最大功率为:P=UI=6V×0.3A=1.8W;
电阻${R}_{1}^{\;}$消耗功率最大功率:P=UI=3V×0.3A=0.9W,故BCD错误;
当滑动变阻器接入电路中的电阻最大时,电路中的电流最小,即:${I}_{1}^{′}=\frac{6}{10+20}=0.2A$
电阻${R}_{1}^{\;}$消耗的最小功率为:$P′=({I}_{1}^{′})_{\;}^{2}{R}_{1}^{\;}=(0.2)_{\;}^{2}×10=0.4W$
则电阻${R}_{1}^{\;}$消耗功率允许的变化范围为0.4W~0.9W,故A正确;
故选:A
点评 本题考查串联电路中电压、电流以及功率、滑动变阻器接入电路电阻的计算,注意求阻值范围时,据电流表和电压表的最大值进行计算,并且会灵活运用欧姆定律.

 阅读快车系列答案
阅读快车系列答案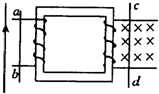 如图所示,ab和cd分别是放在变压器两测光滑水平导轨上的导体,cd静止.通电导线与ab在同一平面内( )
如图所示,ab和cd分别是放在变压器两测光滑水平导轨上的导体,cd静止.通电导线与ab在同一平面内( )| A. | ab向右减速运动时,cd一定向左运动 | |
| B. | ab向右匀速运动时,cd不可能运动 | |
| C. | ab向右加速运动时,cd一定向左运动 | |
| D. | ab向右加速运动时,cd可能不动 |
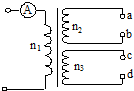 如图所示,变压器输入电压U一定,两个副线圈的匝数分别为n2和n3.当把电热器接在a、b上,使c、d空载时,通过原线圈中的电流表的示数是I0;当把同一电热器接在c、d上,使a、b空载时,电流表的示数为I′,则$\frac{{I}_{0}}{I′}$为( )
如图所示,变压器输入电压U一定,两个副线圈的匝数分别为n2和n3.当把电热器接在a、b上,使c、d空载时,通过原线圈中的电流表的示数是I0;当把同一电热器接在c、d上,使a、b空载时,电流表的示数为I′,则$\frac{{I}_{0}}{I′}$为( )| A. | n2:n3 | B. | n3:n2 | C. | n22:n32 | D. | n32:n22 |
| A. | $\sqrt{\frac{{q}^{3}}{8p}}$ | B. | $\sqrt{\frac{p}{8{q}^{3}}}$ | C. | $\sqrt{\frac{{q}^{3}}{p}}$ | D. | $\sqrt{\frac{p}{{q}^{3}}}$ |
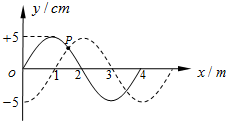 如图所示,一列简谐横波以速度v=10m/s沿x轴正方向传播,实线表示t=0时刻的波形,虚线表示t=0.1s时刻的波形,下列说法正确的是( )
如图所示,一列简谐横波以速度v=10m/s沿x轴正方向传播,实线表示t=0时刻的波形,虚线表示t=0.1s时刻的波形,下列说法正确的是( )| A. | 对于x=0至x=1m之间的质点,在t=0到t=0.1s这段时间内发生的最大位移为5cm | |
| B. | 对于x=0至x=1m之间的质点,在t=0到t=0.1s这段时间内发生的最小位移为5cm | |
| C. | 质点P从t=0时刻起经过0.15s第一次到达波谷 | |
| D. | 质点P从t=0时刻起经过0.25s第一次到达波谷 |
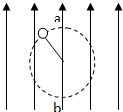 如图,在竖直向上的匀强电场中,一根不可伸长的绝缘细绳的一端系着一个带电小球,另一端固定于O点,小球在竖直平面内做匀速圆周运动,最高点为a,最低点为b,不计空气阻力,则( )
如图,在竖直向上的匀强电场中,一根不可伸长的绝缘细绳的一端系着一个带电小球,另一端固定于O点,小球在竖直平面内做匀速圆周运动,最高点为a,最低点为b,不计空气阻力,则( )| A. | 小球带正电 | |
| B. | 电场力跟重力平衡 | |
| C. | 小球在从a运动到b的过程中,电势能增加 | |
| D. | 小球在运动过程中机械能守恒 |
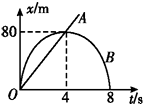
| A. | A质点以20 m/s的速度匀速运动 | |
| B. | B质点最初4 s做加速运动,后4 s做减速运动 | |
| C. | B质点先沿正方向做直线运动,后沿负方向做直线运动 | |
| D. | A、B两质点在4 s末相遇 |
| A. | 只要物体的速度不为零,加速度就不为零 | |
| B. | 只要物体的速度变化量大,加速度就大 | |
| C. | 只要物体的速度大,加速度就大 | |
| D. | 只要物体的速度变化率大,加速度就大 |
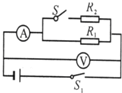 如图所示,当S闭合时,电压表和电流表(均为理想电表)的示数各为1.6V和0.4A.当S断开时,它们的示数各为1.7V和0.3A,求电源的电动势.
如图所示,当S闭合时,电压表和电流表(均为理想电表)的示数各为1.6V和0.4A.当S断开时,它们的示数各为1.7V和0.3A,求电源的电动势.