题目内容
一根长为l的细绳,一端系一小球,另一端悬挂于O点.将小球拉起使细绳与竖直方向成60°角.在O点正下方A、B、C三处先后钉一光滑小钉,使小球由静止摆下后分别被三个不同位置的钉子挡住.已知OA=AB=BC=CD= ,如图所示,则小球继续摆动的最大高度hA,hB,hC(与D点的高度差)之间的关系是( )
,如图所示,则小球继续摆动的最大高度hA,hB,hC(与D点的高度差)之间的关系是( )
A.hA=hB=hC
B.hA>hB>hC
C.hA>hB=hC
D.hA=hB>hC
【答案】分析:由机械能守恒可求得小球在最低点的速度,若摆长大于等于小球下落的高度,则小球可以回到等高点;但若半径较小时,要考虑重力与向心力的关系,分析能否到等高点.
解答:解:小球拉开60°放手,故小球升高的高度为:
h=L-Lcos60°= L
L
由机械能守恒定律可知,由mgh= mv2得:
mv2得:
到达最低点的速度:v= 钉子在A、B两时,小球能摆到等高的位置HA=HB;
钉子在A、B两时,小球能摆到等高的位置HA=HB;
当钉子放在C点时,小球摆到最低点后开始以C点为圆心,以 L为半径做圆周运动,若能到达最高点,最高点处有最小速度,速度不能为零;但由机械能守恒知,如果能到达最高点,速度为零;故小球无法到达最高点;所以上升不到原下落点高度,故HA=HB>HC
L为半径做圆周运动,若能到达最高点,最高点处有最小速度,速度不能为零;但由机械能守恒知,如果能到达最高点,速度为零;故小球无法到达最高点;所以上升不到原下落点高度,故HA=HB>HC
故选D.
点评:在机械能守恒定律的考查中常常和单摆、圆周运动等相结合,要能灵活根据各种运动的不同性质分析可能的能量转化的关系.
解答:解:小球拉开60°放手,故小球升高的高度为:
h=L-Lcos60°=
 L
L由机械能守恒定律可知,由mgh=
 mv2得:
mv2得:到达最低点的速度:v=
 钉子在A、B两时,小球能摆到等高的位置HA=HB;
钉子在A、B两时,小球能摆到等高的位置HA=HB;当钉子放在C点时,小球摆到最低点后开始以C点为圆心,以
 L为半径做圆周运动,若能到达最高点,最高点处有最小速度,速度不能为零;但由机械能守恒知,如果能到达最高点,速度为零;故小球无法到达最高点;所以上升不到原下落点高度,故HA=HB>HC
L为半径做圆周运动,若能到达最高点,最高点处有最小速度,速度不能为零;但由机械能守恒知,如果能到达最高点,速度为零;故小球无法到达最高点;所以上升不到原下落点高度,故HA=HB>HC故选D.
点评:在机械能守恒定律的考查中常常和单摆、圆周运动等相结合,要能灵活根据各种运动的不同性质分析可能的能量转化的关系.

练习册系列答案
相关题目
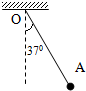 如图所示,用一根长为L的细绳一端固定在O点,另一端悬挂质量为m的小球A,为使细绳与竖直方向夹370角且小球A保持静止状态,则需对小球施加第三个力,下列说法( )
如图所示,用一根长为L的细绳一端固定在O点,另一端悬挂质量为m的小球A,为使细绳与竖直方向夹370角且小球A保持静止状态,则需对小球施加第三个力,下列说法( )A、等于
| ||
B、等于
| ||
| C、等于mg时,一定竖直向上 | ||
| D、以上说法均不正确 |
 光滑水平桌面上有一根长0.4m的细绳l,一端固定在桌上的O点,另一端系一质量为20g的小球(如图所示),小球以2m/s的速度做匀速圆周运动.试求:
光滑水平桌面上有一根长0.4m的细绳l,一端固定在桌上的O点,另一端系一质量为20g的小球(如图所示),小球以2m/s的速度做匀速圆周运动.试求: 如图所示,在圆柱形房屋天花板中心O点悬挂一根长为L的细绳,绳的下端挂一个质量为m的小球,已知绳能承受的最大拉力为2mg,小球在水平面内做圆周运动,当速度逐渐增大到绳断裂后,小球恰好以速度v2=
如图所示,在圆柱形房屋天花板中心O点悬挂一根长为L的细绳,绳的下端挂一个质量为m的小球,已知绳能承受的最大拉力为2mg,小球在水平面内做圆周运动,当速度逐渐增大到绳断裂后,小球恰好以速度v2= 两质量相等的小球A和B,A球挂在一根长为L的细绳O’A上,B球挂在橡皮绳O′B上,现将两球都拉到如图的水平位置上,让两绳均拉直(此时橡皮绳为原长),然后无初速释放,当两球通过最低点O时,橡皮绳与细绳等长,小球A和B速度分别为vA和vB,那么( )
两质量相等的小球A和B,A球挂在一根长为L的细绳O’A上,B球挂在橡皮绳O′B上,现将两球都拉到如图的水平位置上,让两绳均拉直(此时橡皮绳为原长),然后无初速释放,当两球通过最低点O时,橡皮绳与细绳等长,小球A和B速度分别为vA和vB,那么( )