题目内容
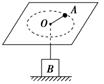
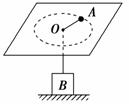
 光滑水平桌面上有一根长0.4m的细绳l,一端固定在桌上的O点,另一端系一质量为20g的小球(如图所示),小球以2m/s的速度做匀速圆周运动.试求:
光滑水平桌面上有一根长0.4m的细绳l,一端固定在桌上的O点,另一端系一质量为20g的小球(如图所示),小球以2m/s的速度做匀速圆周运动.试求:(1)小球做匀速圆周运动的角速度;
(2)若小球从A点运动半圆后,绳碰到一枚钉子B,OB=0.3m,此时绳对球的拉力.
分析:(1)小球在光滑水平面内做匀速圆周运动,由v=ωL求角速度ω.
(2)小球做匀速圆周运动时,由绳子的拉力提供向心力,绳碰到一枚钉子后,线速度不变,半径变化,根据牛顿第二定律求绳子的拉力.
(2)小球做匀速圆周运动时,由绳子的拉力提供向心力,绳碰到一枚钉子后,线速度不变,半径变化,根据牛顿第二定律求绳子的拉力.
解答:解:(1)由v=ωl得:小球运动的角速度ω=
=
=5rad/s
(2)根据牛顿第二定律得:
F=m
=0.02×
=0.89N
答:(1)小球做匀速圆周运动的角速度为5rad/s;
(2)若小球从A点运动半圆后,绳碰到一枚钉子B,OB=0.3m,此时绳对球的拉力为0.89N.
| v |
| L |
| 2 |
| 0.4 |
(2)根据牛顿第二定律得:
F=m
| v2 |
| r |
| 4 |
| 0.09 |
答:(1)小球做匀速圆周运动的角速度为5rad/s;
(2)若小球从A点运动半圆后,绳碰到一枚钉子B,OB=0.3m,此时绳对球的拉力为0.89N.
点评:本题关键要掌握匀速圆周运动的角速度与线速度的关系公式v=ωr,分析向心力的来源,绳碰到一枚钉子后,线速度不变,半径变化,题目比较简单.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
 ?
?