��Ŀ����
����Ŀ����ͼ��ʾ������ΪmA��mB����������A��B���ÿ�������ֵ�ϸ��������������Bѹ��ˮƽ�����ϣ�ʹA�����ģ��߶�ΪH���������Ϸ�ϸ��������ƽ�У��ֳ�ȥѹB��������ʹA��B�Ӿ�ֹ��ʼ�˶���A�ŵغ��������˶�������Bʼ�����������֣�B��ˮƽ�����Ķ�Ħ������Ϊ�̣����ƻ�������䡢���ӵ�Ħ�������ƿ���������ϸ�������ֵ���������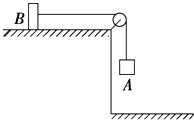
��1��A������̵ļ��ٶȣ�
��2�����ϵ������Ĵ�С��
��3��B���������˶���λ�ƣ�
���𰸡�
��1��
�⣺��ţ�ٵڶ����ɣ�
��A��mAg��T=mAa ��
��B��T����mBg=mBa ��
��ã� ![]() ��
��
��2��
�⣺���۴���٣��ã� ![]()
��3��
�⣺��A���ŵ�ʱAB���ٶ�Ϊv����v2=2aH
��B�� ![]()
��ã� ![]()
B����λ�ƣ� ![]()
����������1���ֱ��A��B������������������ţ�ٵڶ����ɣ�ץס���ٶȴ�С��ȣ����A����ļ��ٶȴ�С����2����A��������������������������ϵ���������3�����A�ŵ�ʱB���ٶȣ��ɶ��ܶ������B�ȼ���ֱ���˶���λ�ƣ��Ӷ��ó��ȼ��ٺ��ȼ���ֱ���˶���λ��֮�ͣ���B���������˶���λ�ƴ�С��
�����㾫����������Ĺؼ���������ܶ������ۺ�Ӧ�õ����֪ʶ������Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݣ�

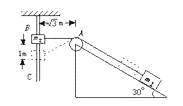
����Ŀ����ͼ��ʾ������ӹ⻬б���ϵ�A���ɾ�ֹ��ʼ�»�������B������ˮƽ�棨�辭��B��ǰ���ٶȴ�С���䣩�����ͣ��C�㣮ÿ��0.2����ͨ���ٶȴ��������������˲ʱ�ٶȣ��������˲��ֲ������ݣ����������ٶ�g=10m/s2����
t��s�� | 0.0 | 0.2 | 0.4 | �� | 1.2 | 1.4 | 1.6 | �� |
v��m/s�� | 0.0 | 1.0 | 2.0 | �� | 1.1 | 0.7 | 0.3 | �� |
��1��б�����Ǧ���
��2��������ˮƽ��֮��Ķ�Ħ�������̣�
��3��t=0.6sʱ��˲ʱ�ٶ�v��