题目内容
【题目】如图，一质量为M、半径为R的光滑大圆环，用一细轻杆固定在竖直平面内；套在大环上质量为m的小环（可视为质点），从大环的最高点处由静止滑下．重力加速度为g．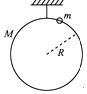
（1）求小环滑到大环最低点处时的动能Ek；
（2）求小环滑到大环最低点处时的角速度ω；
（3）有同学认为，当小环滑到大环的最低点处时，大环对轻杆的作用力与大环的半径R无关，你同意吗？请通过计算说明你的理由．
【答案】
（1）
解：从大环的最高点处由静止滑到最低点过程由动能定理可得：
得：2mgR=Ek﹣0
所以有：Ek=2mgR
（2）
解：由公式Ek= 
mv2
得v=2 
又v=Rω
得ω=2 
（3）
解：在最低点由向心力公式得：
FN﹣mg=m 
求得FN=5mg
由牛顿第三定律得大环受到压力F′
F′=5mg
大环对轻杆作用力F
F=Mg+5mg
说明大环对轻杆的作用力与大环半径R无关．
【解析】（1）从大环的最高点处由静止滑到最低点过程由动能定理求动能；（2）由公式Ek= mv2和v=Rω得ω；（3）在最低点由向心力公式和牛顿第三定律求得大环受到压力，然后判断大环对轻杆的作用力是否与大环半径R无关．
【考点精析】解答此题的关键在于理解动能定理的综合应用的相关知识，掌握应用动能定理只考虑初、末状态，没有守恒条件的限制，也不受力的性质和物理过程的变化的影响.所以，凡涉及力和位移，而不涉及力的作用时间的动力学问题，都可以用动能定理分析和解答，而且一般都比用牛顿运动定律和机械能守恒定律简捷．
练习册系列答案
相关题目
