题目内容
11. 如图所示,竖直平面内固定一个半径为R的半圆形轨道ABC,左端口A和右端口C与圆心O在同一水平面上,M、N为右端口C正上方两点,到右端口C的距离分别为2R和R,现将一小球从M点静止释放,小球从左端口飞出后到达最高处D点,D点与半圆轨道的最低点B的竖直高度差为2R,接着小球又竖直下落返回进入圆弧轨道,若不考虑空气阻力,则下列说法正确的是( )
如图所示,竖直平面内固定一个半径为R的半圆形轨道ABC,左端口A和右端口C与圆心O在同一水平面上,M、N为右端口C正上方两点,到右端口C的距离分别为2R和R,现将一小球从M点静止释放,小球从左端口飞出后到达最高处D点,D点与半圆轨道的最低点B的竖直高度差为2R,接着小球又竖直下落返回进入圆弧轨道,若不考虑空气阻力,则下列说法正确的是( )| A. | 小球返回轨道后能沿轨道一直运动,并上升到N点 | |
| B. | 小球返回轨道后沿轨道运动可能到不了C点 | |
| C. | 小球返回轨道后沿轨道运动到C点时,速度一定大于零 | |
| D. | 若将小球从N点静止释放,则小球恰能运动到左端口A处 |
分析 分析小球在圆形轨道里的受摩擦力做功情况,分析别各过程由动能定理进行分析,则可知小球实际运动情况.
解答 解:A、由题意可知,小球从A点上升没有达到最高点,则说明小球在圆轨道中有阻力做功;故小球在返回过程中同样有阻力做功,小球无法到达N点;故A错误;
B、小球返回轨道后,由于速度小于由C到A过程中的速度,故在轨道里的压力要小,故摩擦力要小,故摩擦力做功小;因此小球能到达C点,并且在C点的速度不为零;故B错误;C正确;
D、由B的分析可知,若将小球由N点释放,则小球一定能超过左端点A处,故D错误;
故选:C.
点评 本题考查动能定理的应用,要注意小球受到的摩擦力与速度有关,速度越快则摩擦力越大,同样的路程上摩擦力做功越多.

练习册系列答案
相关题目
19.如图甲所示的电路中,理想变压器原、副线圈匝数比为10:1,x,y均为理想交流电表,R、L和D分别是光敏电阻(其阻值随光强增大而减小)、理想线圈和灯泡.原线圈接入图乙所示的正弦交流电压M,下列说法中正确的是( )


| A. | 交流电的方向每秒钟改变50次 | |
| B. | 抽出L中的铁芯,A的示数变大 | |
| C. | 有光照射R时,D变暗 | |
| D. | 在t=0.005s时,电压表V的示数为22$\sqrt{2}$V |
3.一束白光垂直于三棱镜的一个面入射发生色散( )
| A. | 棱镜对各色光的折射率不同 | |
| B. | 红光比蓝光通过棱镜所用的时间短 | |
| C. | 黄光比绿光偏转的角度小 | |
| D. | 在棱镜中,速度较大的单色光偏转的角度也较大 |
20.如图所示,三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m, 且与水平方向的夹角均为37°.现有两小物块A、B从传送带顶端都以1m/s的初速度沿传送带两边同时下滑,物块与传送带间的动摩擦因数都是0.5,下列说法正确的是( )
且与水平方向的夹角均为37°.现有两小物块A、B从传送带顶端都以1m/s的初速度沿传送带两边同时下滑,物块与传送带间的动摩擦因数都是0.5,下列说法正确的是( )
 且与水平方向的夹角均为37°.现有两小物块A、B从传送带顶端都以1m/s的初速度沿传送带两边同时下滑,物块与传送带间的动摩擦因数都是0.5,下列说法正确的是( )
且与水平方向的夹角均为37°.现有两小物块A、B从传送带顶端都以1m/s的初速度沿传送带两边同时下滑,物块与传送带间的动摩擦因数都是0.5,下列说法正确的是( )| A. | 物块A先到达传送带底端 | |
| B. | 物块A、B同时到达传送带底端 | |
| C. | 传送带对物块A不做功、对物块B做负功 | |
| D. | 物块A、B在传送带上的划痕长度不相同 |
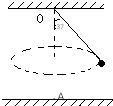 在如图所示的圆锥摆中,已知绳子长度为L=2m,转动过程中与竖直方向夹角为θ=37°,摆球质量为2kg,摆线系于O点,O点离地面的距离OA=2.4m.(g取10m/s2,sin37°=0.6,cos37°=0.8,tan37°=0.75)试求:
在如图所示的圆锥摆中,已知绳子长度为L=2m,转动过程中与竖直方向夹角为θ=37°,摆球质量为2kg,摆线系于O点,O点离地面的距离OA=2.4m.(g取10m/s2,sin37°=0.6,cos37°=0.8,tan37°=0.75)试求: 水平面上静止放置一质量为m=0.2kg的物块,固定在同一水平面上的小型电动机通过水平细线牵引物块,使物块由静止开始做匀加速直线运动,2秒末到达额定功率,其v-t图线如图所示,物块与水平面间的动摩擦因数为μ=0.1,g=10m/s2,电动机与物块间的距离足够远,求:
水平面上静止放置一质量为m=0.2kg的物块,固定在同一水平面上的小型电动机通过水平细线牵引物块,使物块由静止开始做匀加速直线运动,2秒末到达额定功率,其v-t图线如图所示,物块与水平面间的动摩擦因数为μ=0.1,g=10m/s2,电动机与物块间的距离足够远,求: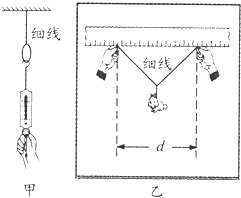 为了较准确的测量某细线能承受的最大拉力,小聪、小明分别进行了如下实验
为了较准确的测量某细线能承受的最大拉力,小聪、小明分别进行了如下实验