Question

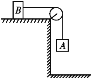
【题目】如图(a)所示，三棱柱的左、右两侧斜面的倾角α=β=45°，物块P、Q用跨过光滑定滑轮的轻绳相连，分别放在两侧的斜面上，此时物块P恰好不向下滑动且物块Q恰不受摩擦力。已知物块P的质量M=2kg，P、Q与斜面之间的动摩擦因数均为μ=0.2，设最大静摩擦力等于滑动摩擦力。

(1)求物块Q的质量m；

(2)如图(b)所示，将三棱柱缓慢绕右侧棱边顺时针转动15°角，物块Q恰好不下滑，求此时物块P所受的摩擦力。

Answer 1

【答案】(1)1.6kg (2)2.256N，方向沿斜面向下

【解析】

（1）三棱柱转动之前，物块P恰好不向下滑动，受到的静摩擦力等于滑动摩擦力，方向沿斜面向上。

设此时绳子弹力为F，分析P的受力，由平衡条件可得

Mgsin α=F+μMgcos α

分析Q的受力由平衡条件可得

F=mgsin β

联立以上两式代入数据解得：

m=1.6 kg。

（2）三棱柱转动15°角后，物块Q恰好不下滑，受到的静摩擦力等于滑动摩擦力，方向沿斜面向上。

设此时绳子弹力为F'，分析Q的受力，由平衡条件可得

mgsin(β+15°)=F'+μmgcos(β+15°)

分析P的受力(设摩擦力大小为Ff，方向沿斜面向上)，由平衡条件可得

Mgsin(α-15°)=F'+Ff

联立以上两式代入数据解得：

Ff=-2.256 N

故物块P所受的摩擦力大小为2.256 N，方向沿斜面向下。