题目内容
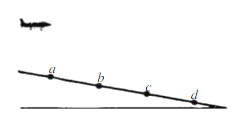
【题目】如图,两光滑平行金属导轨置于水平面(纸面)内,轨间距为l,左端连有阻值为R的电阻.一金属杆置于导轨上,金属杆右侧存在一磁感应强度大小为B、方向竖直向下的匀强磁场区域.已知金属杆以速度v0向右进入磁场区域,做匀变速直线运动,到达磁场区域右边界(图中虚线位置)时速度恰好为零.金属杆与导轨始终保持垂直且接触良好.除左端所连电阻外,其他电阻忽略不计.求金属杆运动到磁场区域正中间时所受安培力的大小及此时电流的功率.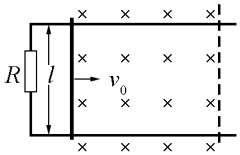
【答案】解:由题意可知,开始时导体棒产生的感应电动势为:E=Blv0 ,
依据闭合电路欧姆定律,则电路中电流为:I= ![]() ,
,
再由安培力公式有:F=BIl= ![]() ;
;
设导体棒的质量为m,则导体棒在整个过程中的加速度为:a= ![]() =
= ![]()
设导体棒由开始到停止的位移为x,由运动学公式:0﹣ ![]()
解得:x= ![]() =
= ![]() ;
;
故正中间离开始的位移为:x中= ![]() ;
;
设导体棒在中间的位置时的速度为v,由运动学公式有:v2﹣v02=2ax中
解得:v= ![]()
则导体棒运动到中间位置时,所受到的安培力为:
F=BIl= ![]() ;
;
导体棒电流的功率为:
P=I2R= ![]() ;
;
答:金属杆运动到磁场区域正中间时所受安培力的大小 ![]() ,及此时电流的功率
,及此时电流的功率 ![]() .
.
【解析】依据法拉第电磁感应定律,求解感应电动势,再结合闭合电路欧姆定律,及安培力表达式,再依据运动学公式,求得中间位置的速度,从而确定安培力大小,最后根据功率表达式,即可求解.
【考点精析】通过灵活运用电磁感应与力学,掌握用法拉第电磁感应定律和楞次定律求感应电动势的大小和方向;求回路中电流强度;分析研究导体受力情况(包含安培力,用左手定则确定其方向);列动力学方程或平衡方程求解即可以解答此题.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案【题目】某同学在研究“对不同物体做相同功情况下,物体质量与速度的关系”时,提出了以下四种猜想: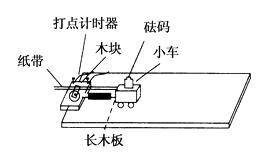
A.m∝v B.m∝ ![]()
C.m∝v2 D.m∝ ![]()
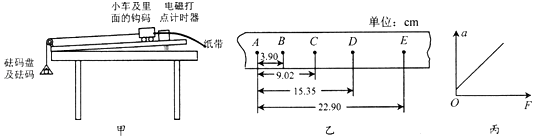
为验证猜想的正确性,该同学用如图所示的装置进行实验:将长木板平放在水平桌面上,木块固定在长木板一端,打点计时器固定在木块上,木块右侧固定一轻弹簧.用连接纸带的小车压缩弹簧至长木板的虚线处由静止释放,打点计时器在纸带上打下一系列点,选取点迹均匀的一部分纸带,计算出小车匀速运动的速度v1 , 测出小车的质量m1;然后在小车上加砝码,再次压缩弹簧至木板虚线处由静止释放小车,计算出小车和砝码匀速运动的速度v2 , 测出小车和砝码的总质量m2;再在小车上加砝码,重复以上操作,分别测出v3、m3……
(1)每次实验中,都将小车压缩弹簧至长木板的虚线处由静止释放,目的是;若要消除每次实验中小车和纸带受到的阻力对小车运动的影响,应进行的实验操作是.
(2)某次实验采集的五组数据如下表:
m/kg | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 |
v/(m·s-1) | 1.000 | 0.707 | 0.577 | 0.500 | 0.447 |
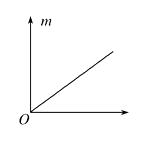
由表格数据直观判断,明显不正确的两个猜想是A、B、C、D中的;若对某个猜想进行数据处理并作图,画出了如图所示的图象,则图中的横坐标应是.