Question

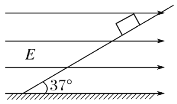
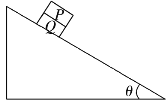
【题目】如图所示，空间中存在垂直于纸面向外的磁感应强度为B的匀强磁场(图中没有画出)，两个质量均为m的物块P、Q叠放在一起，并置于固定在地面上倾角为θ且无限长的绝缘斜面体上。物块P带正电，电荷量为q；物块Q是不带电的绝缘体.P、Q间动摩擦因数为μ1，Q和斜面间动摩擦因数为μ2。现使P、Q一起由静止开始沿斜面下滑，运动过程中P、Q始终保持相对静止。则以下说法正确的是( )

A．根据题设条件可以求出物块P任意时刻的加速度

B．根据题设条件可以求出物块P的最大动能

C．两个物块P、Q间的摩擦力最小值为μ2mgcos θ

D．两个物块P、Q间的摩擦力最小值为μ1mgcos θ

Answer 1

【答案】BC

【解析】由于物体的速度变化时洛伦兹力发生变化，所以除了开始时刻外，其他各时刻P、Q间弹力及摩擦力无法求出，故无法求出任意时刻的加速度，故A错误；根据受力分析可知，P、Q受重力、支持力、摩擦力以及洛伦兹力的作用，由左手定则可知，洛伦兹力垂直斜面向下；物体开始时向下加速运动，随着速度变大，洛伦兹力增大，则压力增大，摩擦力增大；当摩擦力等于重力的分力时物体具有最大动能；此时有：mgsin θ＝μ2[(2m)gcos θ＋Bqv]；由公式可求得最大速度，即可求最大动能；故B正确；对整体分析可知，开始时整体的加速度a＝gsin θ－μ2gcos θ；此时P受摩擦力最小；再对Q分析可知，此时Q受到的摩擦力也为最小值；根据牛顿第二定律可得；摩擦力最小值为：μ2mgcos θ，故C正确，D错误。