题目内容
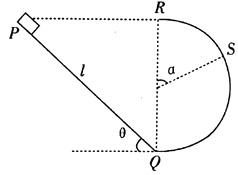
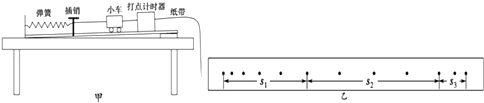
【题目】如图，水平地面和半圆轨道面均光滑，质量M=1kg的小车静止在地面上，小车上表面与R=0.4m的半圆轨道最低点P的切线相平．现有一质量m=2kg的滑块（可视为质点）以v0=7.5m/s的初速度滑上小车左端，二者共速时滑块刚好在小车的最右边缘，此时小车还未与墙壁碰撞，当小车与墙壁碰撞时即被粘在墙壁上，滑块则离开小车进入圆轨道并顺着圆轨道往上运动，已知滑块与小车表面的滑动摩擦因数μ=0.5，g取10m/s2 ． 求：
（1）小车与墙壁碰撞前的速度大小v1；
（2）小车需要满足的长度L；
（3）请判断滑块能否经过圆轨道的最高点Q，说明理由．
【答案】
（1）
解：设滑块与小车的共同速度为v1，滑块与小车相对运动过程中动量守恒，以向右为正方向，由动量守恒定律得：
mv0=（m+M）v1，
代入数据解得：v1=5m/s
（2）
解：设小车的最小长度为L，由系统能量守恒定律得：
，
代入数据解得：L=16.75m
（3）
解：若滑块恰能滑过圆的最高点的速度为v，由牛顿第二定律得：
mg=m 
，
代入数据解得：v=2m/s，
滑块从P运动到Q的过程，根据机械能守恒定律得：
，
代入数据解得：v2=3m/s，v2＞v，说明滑块能过最高点Q
【解析】（1）由动量守恒定律可以求出速度．（2）由能量守恒定律求出小车的长度．（3）由牛顿第二定律与机械能守恒定律分析答题．
【考点精析】根据题目的已知条件，利用动量守恒定律的相关知识可以得到问题的答案，需要掌握动量守恒定律成立的条件：系统不受外力或系统所受外力的合力为零；系统所受的外力的合力虽不为零，但系统外力比内力小得多；系统所受外力的合力虽不为零，但在某个方向上的分量为零，则在该方向上系统的总动量的分量保持不变．
练习册系列答案
相关题目
