题目内容
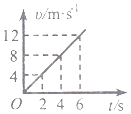
【题目】两滑块a、b沿水平面上同一条直线运动，并发生碰撞；碰撞后两者粘在一起运动；经过一段时间后，从光滑路段进入粗糙路段．两者的位置x随时间t变化的图象如图所示．求：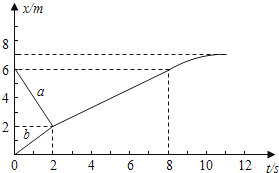
（1）滑块a、b的质量之比；
（2）整个运动过程中，两滑块克服摩擦力做的功与因碰撞而损失的机械能之比．
【答案】
（1）
解：设a、b的质量分别为m1、m2，a、b碰撞前地速度为v1、v2．
由题给的图象得
v1=﹣2m/s①
v2=1m/s②
a、b发生完全非弹性碰撞，碰撞后两滑块的共同速度为v．
由题给的图象得
v= 
m/s③
由动量守恒定律得
m1v1+m2v2=（m1+m2）v④
联立①②③④式得
m1：m2=1：8
答：滑块a、b的质量之比为1：8；
（2）
解：由能量守恒得，两滑块因碰撞损失的机械能为
△E= 
由图象可知，两滑块最后停止运动，
由动能定理得，两滑块克服摩擦力所做的功为
W= 
联立⑥⑦式，并代入数据得
W：△E=1：2
答：整个运动过程中，两滑块克服摩擦力做的功与因碰撞而损失的机械能之比为1：2
【解析】本题是对动量守恒的考查，同时注意位移时间图象的含义，根据图象来计算速度的大小，利用能量的守恒来分析损失的能量的多少．
练习册系列答案
字词句段篇系列答案
相关题目
