题目内容
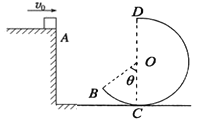
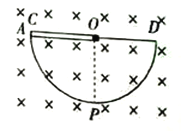
【题目】如图所示，在竖直面内有一半径为L的圆形光滑金属导轨CPD，处于磁感应强度大小为B、方向与导轨平面(纸面)垂直向里的匀强磁场中，圆心为O，直径CD水平，半径OP竖直O、D间用导线连接。一质量分布均匀的金属棒OA，长为L，电阻为R，质量为m，能绕水平轴O在竖直平面内自由转动，棒与导轨和轴O始终接触良好，一切摩擦及其他电阻均不计，重力加速度大小为g。若棒从CO处由静止释放，第一次到达OP处时的角速度为ω，则下列判断正确的是
A. 棒能摆到OD处
B. 从OC到PO的过程中，通过棒横截面的电荷量为
C. 棒第一次到达OP处时，棒中通过的电流为
D. 棒最终会停下，产生的总焦耳热为
mgL
【答案】D
【解析】
A、D、棒沿着导轨摆动切割磁感线而产生动生电动势，导轨与棒组成的回路通电，根据楞次定律可知棒要受到安培阻力，安培力做负功使得机械能变成电能，最终变为通过电阻的焦耳热，则棒第一次不能到达等高的OD处；最终棒通过多个往复的摆动而停在OP处，由能量守恒可知
；故A错误，D正确.
B、从OC到PO的过程中,流过回路的电荷量由
，
，
，故
；故B错误.
C、棒第一次到达OP处时角速度为
，转动产生的平均电动势为
，则电流为
；故C错误.
故选D.
练习册系列答案
名校联盟快乐课堂系列答案
黄冈创优卷系列答案
相关题目
