题目内容
14.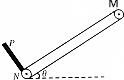 如图所示,一倾斜传送带与水平面的倾角θ=37°,以v=10m/s的速率逆时针方向匀速运行,M、N为传送带的两个端点,MN两点间的距离L=5m,N端有一离传送带很近的弹性挡板P,在传送带上的M处由静止释放质量为1kg的木块(可视为质点),木块与传送带间的动摩擦因数μ=0.5,木块由静止释放后沿传送带向下运动,并与挡板P发生碰撞.已知碰撞时间极短,木块与挡板P碰撞后速度大小为碰撞前的一半,sin37°=0.6,g取10m/s2.传送带与轮子间无相对滑动,不计轮轴处的摩擦.求:
如图所示,一倾斜传送带与水平面的倾角θ=37°,以v=10m/s的速率逆时针方向匀速运行,M、N为传送带的两个端点,MN两点间的距离L=5m,N端有一离传送带很近的弹性挡板P,在传送带上的M处由静止释放质量为1kg的木块(可视为质点),木块与传送带间的动摩擦因数μ=0.5,木块由静止释放后沿传送带向下运动,并与挡板P发生碰撞.已知碰撞时间极短,木块与挡板P碰撞后速度大小为碰撞前的一半,sin37°=0.6,g取10m/s2.传送带与轮子间无相对滑动,不计轮轴处的摩擦.求:(1)木块被释放后经多长时间与挡板P第二次碰撞?
(2)木块运动的总时间和总路程.
分析 (1)根据牛顿第二定律求出物块在下降过程和上升过程中的加速度,运用运动学公式求出下滑过程和上升过程的时间和位移,求出第二次与挡板碰撞的时间;
(2)应用牛顿第二定律与匀变速直线运动的公式求出前几次碰撞的时间和位移.时间和位移按等比规律变化,由数学等比数列求和公式求出总时间和总路程
解答 解:(1)木块相对传送带向上运动,受到沿斜面向下的滑动摩擦力,根据牛顿第二定律,有
$mgsn37°+μmgcos37°=m{a}_{1}^{\;}$
得${a}_{1}^{\;}=gsin37°+μgcos37°=10m/{s}_{\;}^{2}$
设经过时间${t}_{1}^{\;}$,物块与传送带速度相等$v={a}_{1}^{\;}{t}_{1}^{\;}$
得${t}_{1}^{\;}=\frac{v}{{a}_{1}^{\;}}=\frac{10}{10}s=1s$
匀加速运动的位移${x}_{1}^{\;}=\frac{1}{2}{a}_{1}^{\;}{t}_{1}^{2}=\frac{1}{2}×10×{1}_{\;}^{2}=5m$=L,即速度相等时木块与挡板碰撞
木块与挡板碰撞后速度大小为碰撞前的一半,即碰撞后以5m/s反弹,沿传送带向上运动的过程中,根据牛顿第二定律
$mgsin37°+μmgcos37°=m{a}_{2}^{\;}$
解得:${a}_{2}^{\;}=10m/{s}_{\;}^{2}$
向上匀减速的时间${t}_{2}^{\;}=\frac{v′}{{a}_{2}^{\;}}=\frac{5}{10}s=0.5s$
向上匀减速运动的位移${x}_{2}^{\;}=\frac{v{′}_{\;}^{2}}{2{a}_{2}^{\;}}=\frac{{5}_{\;}^{2}}{20}=1.25m$
向下匀加速${a}_{3}^{\;}={a}_{1}^{\;}=10m/{s}_{\;}^{2}$
${x}_{3}^{\;}=\frac{1}{2}{a}_{3}^{\;}{t}_{3}^{2}$
得${t}_{3}^{\;}=\sqrt{\frac{2{x}_{3}^{\;}}{{a}_{3}^{\;}}}=\sqrt{\frac{2×1.25}{10}}=0.5s$
木块被释放后与挡板P第二次碰撞的时间$t={t}_{1}^{\;}+{t}_{2}^{\;}+{t}_{3}^{\;}=1+0.5+0.5=2s$
(2)木块第二次与挡板碰撞的速度${v}_{2}^{\;}=\sqrt{2{a}_{3}^{\;}{x}_{3}^{\;}}=\sqrt{2×10×1.25}=5m/s$
第三次与挡板碰撞后的速度${v}_{3}^{\;}=\frac{1}{2}{v}_{2}^{\;}=(\frac{1}{2})_{\;}^{2}{v}_{1}^{\;}$=2.5m/s
减速到0的时间${t}_{4}^{\;}=\frac{2.5}{10}=0.25s$
向下做匀加速运动的时间${t}_{5}^{\;}={t}_{4}^{\;}=0.25s$
第3次与挡板碰撞后向上匀减速运动的位移${x}_{4}^{\;}=\frac{{v}_{3}^{2}}{2{a}_{3}^{\;}}=\frac{2.{5}_{\;}^{2}}{20}=0.3125$m
总时间t=1+0.5+0.5+0.25+0.25+0.125+0.125+…=3s
总路程s=5+1.25+1.25+0.3125+0.3125+…═$8\frac{1}{3}m$
答:(1)木块被释放后经2s时间与挡板P第二次碰撞
(2)木块运动的总时间3s和总路程$8\frac{1}{3}m$
点评 本题为多过程多物体问题,过程较为复杂,解题的关键理清每一段过程,分别运用牛顿定律和运动学知识进行分析求解即可;要求思路要清晰,按步骤一步步进行即可求解.

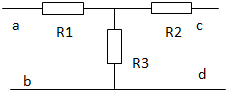 一个T型电路如图,电路中的电阻R1=10Ω,R2=120Ω,R3=40Ω,另有一测试电源,电动势为100V,内阻忽略不计,则( )
一个T型电路如图,电路中的电阻R1=10Ω,R2=120Ω,R3=40Ω,另有一测试电源,电动势为100V,内阻忽略不计,则( )| A. | 当cd端短路时,ab之间的等效电阻是130Ω | |
| B. | 当ab端短路时,cd之间的等效电阻是130Ω | |
| C. | 当ab端接通测试电源时,cd之间的电压为80V | |
| D. | 当cd端接通测试电源时,ab之间的电压为80V |
| A. | 刹车后6s末的速度为2m/s | |
| B. | 刹车后6s内的位移为25m | |
| C. | 刹车中整个位移中点的速度约为7.1m/s | |
| D. | 停止前最后第3s、第2s、最后1s的位移之比为1:3:5 |
| A. | 牛顿通过理想斜面实验总结出力是改变物体运动状态的原因 | |
| B. | 开普勒用20年的时间研究第谷的行星观测记录,总结出了开普行星运动定律 | |
| C. | 第2s末到第4s初的时间间隔是1s | |
| D. | 物体在力的作用下形状或体积发生的改变,叫做弹性形变 |
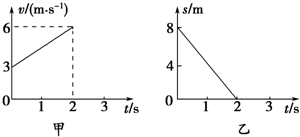 有一个质量为4kg的质点在x-y平面内运动,在x方向的速度图象和y方向的位移图象分别如图甲、乙所示,下列说法正确的是( )
有一个质量为4kg的质点在x-y平面内运动,在x方向的速度图象和y方向的位移图象分别如图甲、乙所示,下列说法正确的是( )| A. | 质点做匀变速直线运动 | B. | 质点所受的合外力为22 N | ||
| C. | 2 s时质点的速度为6 m/s | D. | 0时刻质点的速度为5 m/s |
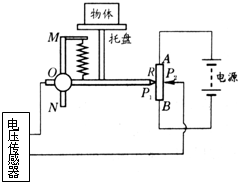 如图所示为某种测量物体质量的装置示意图,AB为一均匀的滑动变阻器,总阻值为R,长度为L,两边分别有P1、P2 两个滑动头,P1 可在竖直绝缘光滑的固定杆MN上保持水平状态而上下自由滑动.若P1、P2间出现电压时,可通过电压传感器测量出该电压U的大小.所用弹簧受到外力的大小与形变量的比值恒为已知值k,托盘自身质量不可忽略,电源电动势为E,内阻不计,当地的重力加速度为g.现用该装置测量待测物体的质量mx:
如图所示为某种测量物体质量的装置示意图,AB为一均匀的滑动变阻器,总阻值为R,长度为L,两边分别有P1、P2 两个滑动头,P1 可在竖直绝缘光滑的固定杆MN上保持水平状态而上下自由滑动.若P1、P2间出现电压时,可通过电压传感器测量出该电压U的大小.所用弹簧受到外力的大小与形变量的比值恒为已知值k,托盘自身质量不可忽略,电源电动势为E,内阻不计,当地的重力加速度为g.现用该装置测量待测物体的质量mx: 如图,一上端开口、下端封闭的细长玻璃管竖直放置.玻璃管的下部封有长ll=25.0cm的空气柱,中间有一段长为l2=25.0cm的水银柱,上部空气柱的长度l3=40.0cm.已知大气压强为P0=75.0cmHg.现将一活塞(图中未画出)从玻璃管开口处缓缓往下推,使管下部空气柱长度变为l'1=20.0cm.假设活塞下推过程中没有漏气,求活塞下推的距离.
如图,一上端开口、下端封闭的细长玻璃管竖直放置.玻璃管的下部封有长ll=25.0cm的空气柱,中间有一段长为l2=25.0cm的水银柱,上部空气柱的长度l3=40.0cm.已知大气压强为P0=75.0cmHg.现将一活塞(图中未画出)从玻璃管开口处缓缓往下推,使管下部空气柱长度变为l'1=20.0cm.假设活塞下推过程中没有漏气,求活塞下推的距离.