题目内容
8.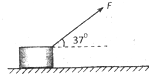 如图所示,质量为m=0.78kg的金属块放在水平桌面上,在与水平方向成θ=37°角斜向上、大小为F=3.0N的拉力作用下,以v=2.0m/s的速度向右做匀速直线运动.己知sin37°=0.60,cos37°=0.80.g取10m/s2,求;
如图所示,质量为m=0.78kg的金属块放在水平桌面上,在与水平方向成θ=37°角斜向上、大小为F=3.0N的拉力作用下,以v=2.0m/s的速度向右做匀速直线运动.己知sin37°=0.60,cos37°=0.80.g取10m/s2,求;(1)金属块与桌面间的动摩擦因数μ;
(2)如果从某时刻起撤去拉力,从该时刻起再经过t=5s,金属块在桌面上滑行的距离s.
分析 (1)金属块受到重力mg、拉力F、地面的支持力和滑动摩擦力作用,根据力平衡条件和滑动摩擦力公式求出求出μ.
(2)撤去拉力,金属块水平方向受到滑动摩擦力作用而做匀减速运动,要根据牛顿第二定律求出加速度,再根据速度公式求出时间.
解答 解:(1)设在拉力作用下金属块所受地面的支持力为N,滑动摩擦力为f,则根据平衡条件得
Fcos37°=f
Fsin37°+N=mg
又f=μN
联立解得:μ=0.4
(2)撤去拉力F后,金属块受到滑动摩擦力为:f′=μmg
根据牛顿第二定律,得加速度大小为:a=f′m=μmgmf'm=μmgm=μg=0.4×10=4m/s2
则撤去F后金属块还能滑行的时间为:t0=0−v−a=0−2−4=0.5s<5s
所以金属块在5s内的位移等于0.5s内的位移,位移为:s=v22a=222×4=0.5m
答:(1)金属块与桌面间的动摩擦因数?为0.4;
(2)撤去拉力后从该时刻起再经过t=5s,金属块在桌面上滑行的距离为0.5m.
点评 本题是牛顿第二定律和力平衡条件的简单综合,要防止产生这样的错误解答:在拉力F作用时f=μmg.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18. 国庆节时,五颜六色的氢气球将节日装扮得靓丽多姿.如图所示,一氢气球通过软绳与地面上的石块相连,石块质量为m,由于风的作用,使软绳偏离竖直方向,当氢气球和石块相对地面静止时,与石块相连的绳端切线与水平方向成θ角,不计风对石块的作用,则下列说法中正确的是( )
国庆节时,五颜六色的氢气球将节日装扮得靓丽多姿.如图所示,一氢气球通过软绳与地面上的石块相连,石块质量为m,由于风的作用,使软绳偏离竖直方向,当氢气球和石块相对地面静止时,与石块相连的绳端切线与水平方向成θ角,不计风对石块的作用,则下列说法中正确的是( )
 国庆节时,五颜六色的氢气球将节日装扮得靓丽多姿.如图所示,一氢气球通过软绳与地面上的石块相连,石块质量为m,由于风的作用,使软绳偏离竖直方向,当氢气球和石块相对地面静止时,与石块相连的绳端切线与水平方向成θ角,不计风对石块的作用,则下列说法中正确的是( )
国庆节时,五颜六色的氢气球将节日装扮得靓丽多姿.如图所示,一氢气球通过软绳与地面上的石块相连,石块质量为m,由于风的作用,使软绳偏离竖直方向,当氢气球和石块相对地面静止时,与石块相连的绳端切线与水平方向成θ角,不计风对石块的作用,则下列说法中正确的是( )| A. | 绳子的拉力为mgsinθ | |
| B. | 绳子的拉力一定小于mg,否则石块将会被风吹动的氢气球带离地面 | |
| C. | 石块受到地面作用力不等于绳子拉力的水平分力 | |
| D. | 石块受到地面作用力和绳子拉力的合力大于石块的重力 |
19.如图是甲、乙两质点的V-t,图象,则由图可知( )


| A. | 0时刻乙的速度大 | B. | 甲、乙两质点都做匀加速直线运动 | ||
| C. | 在相等的时间内甲的速度变化大 | D. | 在前5s内乙的速度大 |
16.关于简谐振动,下列说法正确的是( )
| A. | 如果质点振动的位移与时间的关系遵从正弦函数的规律,这样的振动叫做简谐振动 | |
| B. | 如果质点做简谐振动,则质点振动的动能和弹性势能的总和保持不变 | |
| C. | 回复力F=-kx,是简谐振动的条件,回复力F只能是弹力 | |
| D. | 弹簧振子的振动在考虑空气阻力时,做的也是简谐振动 |
3.如图,将甲、乙两个相同的条形磁铁吸在一起,置于桌面上,下面说法正确的是( )


| A. | 甲对乙的压力等于甲的重力 | B. | 甲对乙的压力大于甲的重力 | ||
| C. | 乙对桌面的压力等于甲乙的总重力 | D. | 乙对桌面的压力小于甲乙的总重力 |
13. 如图所示,斜劈劈尖顶着竖直墙壁静止于水平面上,现将一小球从图示位置静止释放,不计一切摩擦,则在小球从释放到落至地面的过程中,下列说法正确的是( )
如图所示,斜劈劈尖顶着竖直墙壁静止于水平面上,现将一小球从图示位置静止释放,不计一切摩擦,则在小球从释放到落至地面的过程中,下列说法正确的是( )
 如图所示,斜劈劈尖顶着竖直墙壁静止于水平面上,现将一小球从图示位置静止释放,不计一切摩擦,则在小球从释放到落至地面的过程中,下列说法正确的是( )
如图所示,斜劈劈尖顶着竖直墙壁静止于水平面上,现将一小球从图示位置静止释放,不计一切摩擦,则在小球从释放到落至地面的过程中,下列说法正确的是( )| A. | 斜劈对小球的弹力做负功 | |
| B. | 斜劈与小球组成的系统机械能不守恒 | |
| C. | 小球的机械能守恒 | |
| D. | 斜劈机械能守恒 |
17.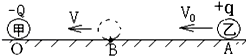 如图所示,一个电量为-Q的点电荷甲,固定在绝缘水平面上的O点.另一个电荷量为+q及质量为m的点电荷乙,从A点以初速度v0沿它们的连线向甲运动,运动到B点时的速度为v,且为运动过程中速度最小值.已知点电荷乙与水平面的动摩擦因数为μ,AB间距离为L0,静电力常量为k,则下列说法正确的是( )
如图所示,一个电量为-Q的点电荷甲,固定在绝缘水平面上的O点.另一个电荷量为+q及质量为m的点电荷乙,从A点以初速度v0沿它们的连线向甲运动,运动到B点时的速度为v,且为运动过程中速度最小值.已知点电荷乙与水平面的动摩擦因数为μ,AB间距离为L0,静电力常量为k,则下列说法正确的是( )
 如图所示,一个电量为-Q的点电荷甲,固定在绝缘水平面上的O点.另一个电荷量为+q及质量为m的点电荷乙,从A点以初速度v0沿它们的连线向甲运动,运动到B点时的速度为v,且为运动过程中速度最小值.已知点电荷乙与水平面的动摩擦因数为μ,AB间距离为L0,静电力常量为k,则下列说法正确的是( )
如图所示,一个电量为-Q的点电荷甲,固定在绝缘水平面上的O点.另一个电荷量为+q及质量为m的点电荷乙,从A点以初速度v0沿它们的连线向甲运动,运动到B点时的速度为v,且为运动过程中速度最小值.已知点电荷乙与水平面的动摩擦因数为μ,AB间距离为L0,静电力常量为k,则下列说法正确的是( )| A. | 点电荷乙从A点运动到B点的过程中,加速度逐渐减小 | |
| B. | OB间的距离为√kQqμmg | |
| C. | 点电荷乙越过B点向左运动,其电势能仍增多 | |
| D. | 在点电荷甲形成的电场中,AB间电势差UAB=μmgL0+12mv2−12mv02q |
 如图所示,竖直放置的轻弹簧上端与质量为3kg的物块B相连接,另一个质量为1kg的物块A放在B上.先向下压A,然后释放,A、B共同向上运动一段后将分离,分离后A又上升了0.2m到达最高点,此时B的速度方向向下,且弹簧恰好为原长.从A、B分离到A上升到最高点的过程中,弹簧弹力对B做的功及弹簧回到原长时B的速度大小分别是(g=10m/s2)( )
如图所示,竖直放置的轻弹簧上端与质量为3kg的物块B相连接,另一个质量为1kg的物块A放在B上.先向下压A,然后释放,A、B共同向上运动一段后将分离,分离后A又上升了0.2m到达最高点,此时B的速度方向向下,且弹簧恰好为原长.从A、B分离到A上升到最高点的过程中,弹簧弹力对B做的功及弹簧回到原长时B的速度大小分别是(g=10m/s2)( )