Question

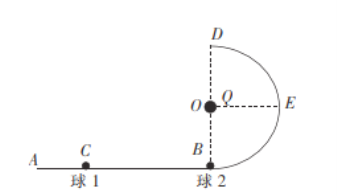
【题目】一光滑绝缘轨道ABD固定在竖直平面上，如图所示，AB段水平，BD段是半径为R的半圆弧，有一电荷量为Q的正点电荷固定在圆心O点。一质量为m，不带电的小球1放在绝缘轨道上，在水平外力作用下从C点由静止开始运动，到B点时撤去外力，与静止在B处的另一质量为m，带电荷量为+q的小球2发生正碰，碰撞过程中小球1的动量改变量大小始终为碰前球1动量的。已知CB之间的距离为2R，且碰幢过程中不交换电荷量。

(1)若水平外力为恒力，求碰幢前球1的速度大小；

(2)若水平外力为恒力，求碰幢后球2在E点对轨道的压力；

(3)若碰幢后球2要能运动到D点，求F的最小值。

Answer 1

【答案】(1)(2)(3)；

【解析】

(1)到由动能定理得：

解得：

(2)由于球1动量的改变量为碰幢前球1动量的 ，因此球1的速度变为

由动量守恒定律得：

球2的速度为：

到，电场力不做功，由动能定理得：

解得：

由牛顿第二定律得：

解得：

根据牛顿第三定律，小球对轨道的压力为，方向向右

(3)为使球2能过点，求的最小值，即刚好过最高点

(i )若

到达最高点时速度应为零

由动能定理得：

球2在点的速度为：

根据动量守恒定律，球1碰前的速度为：

到由动能定理得：

解得：

(ii)若

到达最高点时速度应大于等于即可

由动能定理得：

球2在点的速度为：

根据动量守恒定律，球1碰前的速度为：

到由动能定理得：

解得：