题目内容
【题目】在匀强磁场中有一个原来静止的碳14原子核，它发生衰变放射出的粒子X与反冲核氮14分别在磁场中做匀速圆周运动，则：（ ）
A. 放射出的粒子与反冲核在磁场中运动的轨迹互为外切圆
B. 粒子X与反冲核的运动周期之比为7：1
C. 粒子X与反冲核的轨迹半径之比为7：1
D. 衰变过程中动量守恒，机械能守恒
【答案】C
【解析】根据电荷数和质量数守恒分析碳（
）放射出的粒子是
粒子（
）．原子核的衰变过程满足动量守恒，知粒子与反冲核的速度方向相反，根据左手定则判断得知，粒子与反冲核的旋转方向相反，反冲核的轨迹与粒子的轨迹是内切圆，如图所示：
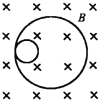
故A错误．根据
，可知
，故B错误；根据动量守恒定律知：两带电粒子动量大小相等，方向相反，即有：
，由带电粒子在匀强磁场中圆周运动的半径公式可得：
，可知r与q成反比．粒子与反冲核的电荷量之比为1：7．所以粒子与反冲核的轨道半径之比为7：1，故C正确；碳（）原子核衰变时要放出核能，所以机械能不守恒，而动量是守恒的，故D错误．故选C.
练习册系列答案
世纪百通期末金卷系列答案
相关题目
