题目内容
【题目】如图所示有一个圆环形区域,区域内有垂直纸面向里的匀强磁场,已知其截面内半径为R1=1.0 m,磁感应强度为B=1.0 T,被约束粒子的比荷为![]() =4.0×107C/kg,该带电粒子从中空区域与磁场交界面上的P点以速度v0=4.0×107m/s沿环的半径方向射入磁场(不计带电粒子在运动过程中的相互作用,不计带电粒子的重力).求
=4.0×107C/kg,该带电粒子从中空区域与磁场交界面上的P点以速度v0=4.0×107m/s沿环的半径方向射入磁场(不计带电粒子在运动过程中的相互作用,不计带电粒子的重力).求

(1)粒子在磁场中做圆周运动的半径r
(2)如果被约束粒子不穿越磁场外边界,求磁场区域的最小外半径R2.
【答案】(1)1.0m (2)2.41 m
【解析】试题分析:粒子在磁场中做圆周运动时,洛伦兹力提供向心力,根据![]() ,即可粒子在磁场中做圆周运动的半径r;粒子垂直进入磁场中做匀速圆周运动,当该粒子的轨迹恰好与圆形区域外边界相切时,磁场区域的半径最小,根据牛顿第二定律求出粒子圆周运动的半径,由几何知识求出磁场区域的最小外半径R2。
,即可粒子在磁场中做圆周运动的半径r;粒子垂直进入磁场中做匀速圆周运动,当该粒子的轨迹恰好与圆形区域外边界相切时,磁场区域的半径最小,根据牛顿第二定律求出粒子圆周运动的半径,由几何知识求出磁场区域的最小外半径R2。
(1)粒子在磁场中做圆周运动时,洛伦兹力提供向心力: ![]()
解得: ![]()
代入数据可得:r=1.0m
(2)粒子运动轨迹如图所示:
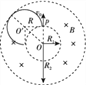
由几何关系得R2=![]() R1+r
R1+r
解得: ![]()

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目