题目内容
某型号汽车发动机的额定功率P0=60kW，汽车质量m=1×103kg，在水平路面上正常行驶中所受到的阻力大小恒为车重的0.15倍．g取10m/s2．
（1）求该汽车在水平路面上行驶能达到的最大速度vm；
（2）若该汽车由静止开始以a1=0.5m/s2的加速度匀加速行驶，求维持汽车做匀加速直线运动的时间t；
（3）若该汽车在水平高速公路上以v=36m/s的速度匀速行驶，轮胎与路面的动摩擦因数μ=0.60，驾驶员的反应时间△t=0.50s，求驾驶员驾驶该汽车与前车保持的安全距离的最小值s．
（1）求该汽车在水平路面上行驶能达到的最大速度vm；
（2）若该汽车由静止开始以a1=0.5m/s2的加速度匀加速行驶，求维持汽车做匀加速直线运动的时间t；
（3）若该汽车在水平高速公路上以v=36m/s的速度匀速行驶，轮胎与路面的动摩擦因数μ=0.60，驾驶员的反应时间△t=0.50s，求驾驶员驾驶该汽车与前车保持的安全距离的最小值s．
（1）当汽车发动机达到额定功率并做匀速运动时，汽车达到最大速度，此时发动机牵引力为：
F=f1=kmg=0.15×1×103=1.5×103N，
则vm=
=
=40m/s
（2）设汽车匀加速行驶时发动机牵引力为F1，根据牛顿第二定律有：
F1-f1=ma1
得：F1=f1+ma1=1500+1000×0.5=2×103N
维持汽车做匀加速直线运动的最大速度
vm1=
=
=30m/s
维持汽车做匀加速直线运动的时间为：
t=
=
=60s
（3）当出现紧急情况时，汽车刹车时受到的总阻力为：
f=f1+μmg=1500+0.6×10000=7.5×103N
此时汽车的加速度大小为：a2=
=
=7.5m/s2
汽车在司机反应时间内匀速行驶的距离为：s1=v△t=36×0.5=18m
由v2=2a2s2得汽车的刹车距离为：s2=
=
=86.4m
所以此汽车与前车保持的安全距离的最小值为：s=s1+s2=18+86.4=104.4m
答：（1）该汽车在水平路面上行驶能达到的最大速度为40m/s；
（2）维持汽车做匀加速直线运动的时间为60s；
（3）驾驶员驾驶该汽车与前车保持的安全距离的最小值为104.4m．
F=f1=kmg=0.15×1×103=1.5×103N，
则vm=
| P0 |
| F |
| 60000 |
| 1500 |
（2）设汽车匀加速行驶时发动机牵引力为F1，根据牛顿第二定律有：
F1-f1=ma1
得：F1=f1+ma1=1500+1000×0.5=2×103N
维持汽车做匀加速直线运动的最大速度
vm1=
| P0 |
| F1 |
| 60000 |
| 2000 |
维持汽车做匀加速直线运动的时间为：
t=
| vm1 |
| a1 |
| 30 |
| 0.5 |
（3）当出现紧急情况时，汽车刹车时受到的总阻力为：
f=f1+μmg=1500+0.6×10000=7.5×103N
此时汽车的加速度大小为：a2=
| f |
| m |
| 7500 |
| 1000 |
汽车在司机反应时间内匀速行驶的距离为：s1=v△t=36×0.5=18m
由v2=2a2s2得汽车的刹车距离为：s2=
| v2 |
| 2a2 |
| 362 |
| 2×7.5 |
所以此汽车与前车保持的安全距离的最小值为：s=s1+s2=18+86.4=104.4m
答：（1）该汽车在水平路面上行驶能达到的最大速度为40m/s；
（2）维持汽车做匀加速直线运动的时间为60s；
（3）驾驶员驾驶该汽车与前车保持的安全距离的最小值为104.4m．
练习册系列答案
步步高达标卷系列答案
相关题目
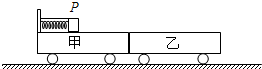处于静止状态．两车之间有一感应机关，在它的作用下，当滑块滑过两车连接处时，两车将自动分离．现剪断细线，滑块先后在甲、乙小车上滑行，最终滑块恰好滑到乙车的另一端而未滑出乙车．取g=10m/s2，求：